- #1
MNWO
- 10
- 0
Hello, so I've been given this question and I get a different anwser then my friends. Can you check if what I wrote is right? If its wrong then can you tell me what have I done wrong? Sorry for the quality of the picture but my Paint skills are not so great :)
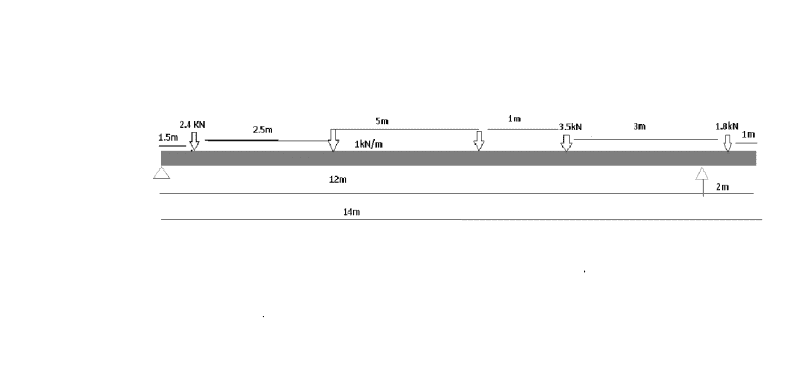 I was measuring to the right support
I was measuring to the right support
RA is the left support, RB is the right support. Here is my calculations:
Sum of anticlockwise movement = Sum of clockwise movement
forces to the right support= 2.4 + 5 + 3.5 = 10.9kN
force x distance to the support= (3.5kN x 2m) + ( 5kN x 5.5m) + (2.4kN x 10.5m)=59.7kN
59.7kN=sum of clockwise movement
1.8kN + RB12 = 59.7kN
59.7-1.8=57.9kN
57.9/12=RB
RB=4.825
so RA= 59.7kN- 4.825
RA=54.875 kN
RA is the left support, RB is the right support. Here is my calculations:
Sum of anticlockwise movement = Sum of clockwise movement
forces to the right support= 2.4 + 5 + 3.5 = 10.9kN
force x distance to the support= (3.5kN x 2m) + ( 5kN x 5.5m) + (2.4kN x 10.5m)=59.7kN
59.7kN=sum of clockwise movement
1.8kN + RB12 = 59.7kN
59.7-1.8=57.9kN
57.9/12=RB
RB=4.825
so RA= 59.7kN- 4.825
RA=54.875 kN
Last edited by a moderator: