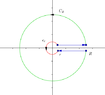
Let $\varepsilon > 0$ be small and $R>0$ be large.
1) Start at $i\varepsilon$, in the clockwise direction draw semicircle $C$ centered at $0$ that ends at $-i\varepsilon$.
2) Draw rays emanating at $\pm i\varepsilon$, endpoints of $C$, to the left, so $-t\pm i\varepsilon $ for $t\geq 0$.
3) Draw circle $\Gamma$ centered at $0$ of radius $R$.
4) The rays intersect $\Gamma$ at points $\alpha,\beta$ with $\text{Im}(\alpha) > \text{Im}(\beta)$.
Now define $\Gamma_1$ as contour starting at $\beta$, travel counterclockwise along $\Gamma$ until reaching $\alpha$. Travel linearly along ray until reaching $i\varepsilon$. Then move clockwise along $C$ until reaching $-i\varepsilon$. Then travel linearly along ray until returning back to $\alpha$.
Define the function,
$$ f(z) = \frac{\log z}{z^2 + 1} $$
Where $\log z$ is the principal logarithm and integrate,
$$ \oint_{\Gamma_1} f(z) ~ dz $$