hnes
- 4
- 0
Hi!
According to the book "Renewable Energy on Power Systems" by Freris & Infield, the voltage rise due to injection of power in pcc can be estimated from the Thevenin equivalent representing the network "upstream" pcc (Figure 1). The Thevenin voltage can be taken as the nominal voltage in the pcc, and the Thevenin impedance
is given by Z= V/√3⋅Isc (1).
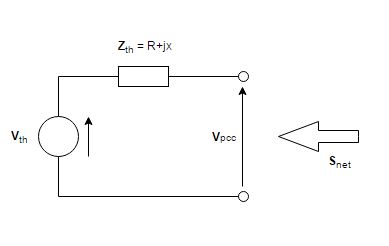
Figure 1: Thevenin equivalent
I've got some measured fault current values (three phase) for different Pcc's in different LV radial distribution networks, and want to make an estimate of the voltage rise in each Pcc based on the calculated source impedance in formula 1. This is pretty straight forward according to the mentioned literature, but there is something i don't get:
Is the fault current in the Pcc depending on the numbers of other buses in the LV radial? For me it seems pretty obvious that the impedance seen from the Pcc with DG is lower if your neighbor has a big demand of power, and thus the voltage rise in the Pcc will become smaller (?). I don't get how this Zth calculated from the Isc can be used if this is not the case.
PS: I probably lack some understanding in source impedance and fault levels.
<< Edit -- clarification of PCC definition >>
Point of Common Coupling - the point where the the generator is connected to the public grid.
According to the book "Renewable Energy on Power Systems" by Freris & Infield, the voltage rise due to injection of power in pcc can be estimated from the Thevenin equivalent representing the network "upstream" pcc (Figure 1). The Thevenin voltage can be taken as the nominal voltage in the pcc, and the Thevenin impedance
is given by Z= V/√3⋅Isc (1).
Figure 1: Thevenin equivalent
I've got some measured fault current values (three phase) for different Pcc's in different LV radial distribution networks, and want to make an estimate of the voltage rise in each Pcc based on the calculated source impedance in formula 1. This is pretty straight forward according to the mentioned literature, but there is something i don't get:
Is the fault current in the Pcc depending on the numbers of other buses in the LV radial? For me it seems pretty obvious that the impedance seen from the Pcc with DG is lower if your neighbor has a big demand of power, and thus the voltage rise in the Pcc will become smaller (?). I don't get how this Zth calculated from the Isc can be used if this is not the case.
PS: I probably lack some understanding in source impedance and fault levels.
<< Edit -- clarification of PCC definition >>
Point of Common Coupling - the point where the the generator is connected to the public grid.
Last edited by a moderator: