- #1
Diagram pressure forces over a body resting on an inclined surface
Click For Summary
SUMMARY
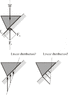
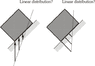
This discussion focuses on the behavior of diagram pressure forces acting on a body, specifically a prism resting on an inclined surface. It is established that pressure acts in a straight line, normal to the surface, and only the normal reaction force contributes to this pressure. The conversation highlights the complexity of calculating reaction forces in systems with multiple supports, emphasizing that additional equations may be necessary to determine all forces accurately. The internal structure of the prism is crucial for understanding the specific pressure diagram.
PREREQUISITES- Understanding of basic mechanics and forces
- Familiarity with reaction forces and their calculations
- Knowledge of torque and its application in static systems
- Concept of elasticity in materials
- Research the principles of static equilibrium in mechanics
- Study the calculation of reaction forces in multi-support systems
- Explore torque calculations in inclined planes
- Learn about the elasticity of materials and its impact on structural integrity
Students and professionals in engineering, particularly those focusing on mechanics, structural analysis, and material science, will benefit from this discussion.
- #2
rock.freak667
Homework Helper
- 6,221
- 31
...well yes essentially pressure acts in a straight line, normal to a surface. In the diagram, only the component of the force reaction surface (the force normal reaction) would exert a pressure.
- #3
Bob S
- 4,662
- 8
You might want to consider a torque about the CM, because the friction force does not act on CM, while the gravitational force does.
- #4
- #5
tiny-tim
Science Advisor
Homework Helper
- 25,837
- 258
orlan2r said:
Hi orlan2r!
You're asking about the line formed by the ends of the vectors representing the reaction force at each point, as shown in the diagrams.
So far as I know, it is assumed that the ends lie along a line, but there is no mathematical way to prove this.
Consider a beam supported at two points … there are two independent equations, from which we can find the two reaction forces.
But if the beam is supported at three points, there are still only two independent equations, but there are three reaction forces.
We can only find those three forces if we include a third equation, which in that case will describe the elasticity of the beam.
Similarly, we usually assume that a table supported on four legs has four equal reaction forces. But that need not be so, as is easily seen by cutting one of the legs … the table can still stand on three legs!
We cannot say what the "diagram pressure" will be for your prism, unless we know the internal structure of the prism.