Diagramming the Integral: A Visual Guide

[mmh37]

Problem:

"Draw a Diagram to show over which area the following integral (see integral in attached file) is integrated."

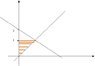
I drew a little diagram of what I think the area looks like (see diagram). But I am very, very insecure about what I did and would appreciate if anyone could have a look at it and let me know if I did something wrong. That would be really helpful!

 

[TD]

I can't see the attachments yet, perhaps you could give the integral and the area? Try LaTeX

 

[mmh37]

$$\int {2x^2+y} dxdy$$

and the boundary conditions are

for x: y < x < 2-y

for y: 0 < y < 1

hope that helps

 

[HallsofIvy]

The outer integral is y so first draw to horizontal lines at y= 0 and y= 1 to define the limits for y. Now, for each y, x lies between y= x and x= 2- y which is the same as y= 2- x. However, in your picture you have x running between 0 and x. Move your stripes (indicating the figure) to the triangle formed by y= x, y= 2- x, and y= 0. (0f course, you notice that y= 2- x and y= x cross at y= 1.)

 

[mmh37]

thanks for this!

I'm not sure whether this second attempt is right, but here is the new diagram anyway (with inverted strips):