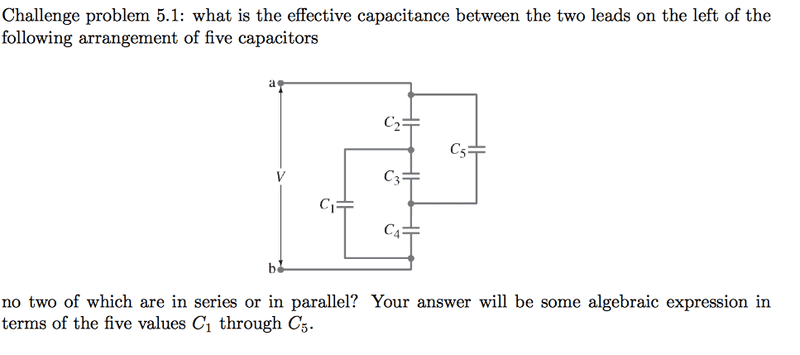
SUMMARY
The discussion centers on solving a complex introductory electricity circuit problem involving capacitors. Participants suggest using the equation Q = C V to calculate charge across multiple capacitors arranged in a non-standard configuration. The challenge arises from the lack of series or parallel arrangements among the capacitors, complicating the application of standard methods. Participants recommend using Kirchhoff's Current Law (KCL) to derive equations for the circuit, emphasizing the importance of understanding the unique arrangement of different capacitances.
PREREQUISITES
- Understanding of capacitor behavior and the equation Q = C V
- Familiarity with circuit analysis techniques, including Kirchhoff's Current Law (KCL)
- Knowledge of Wheatstone bridge configurations
- Basic principles of series and parallel capacitor combinations
NEXT STEPS
- Research advanced capacitor circuit analysis techniques
- Study the application of Kirchhoff's Current Law in complex circuits
- Learn about Wheatstone bridge principles and their applications in capacitor circuits
- Explore methods for calculating equivalent capacitance in non-standard configurations
USEFUL FOR
Students studying electrical engineering, educators teaching circuit analysis, and anyone seeking to deepen their understanding of capacitor behavior in complex circuits.