Homework Help Overview
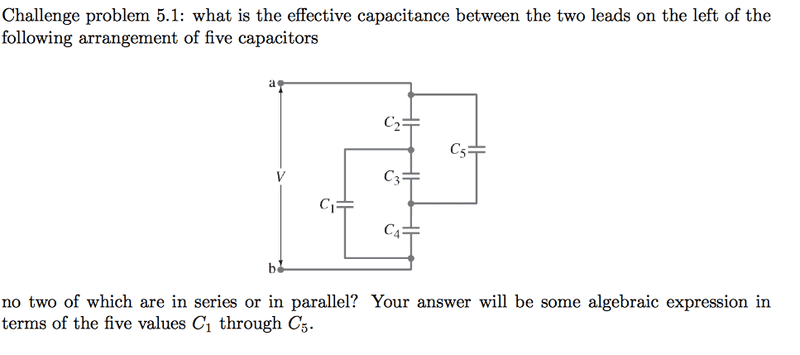
The discussion revolves around a challenging introductory electricity circuit problem involving capacitors. Participants are exploring the configuration of capacitors and their relationships in a circuit that resembles a Wheatstone bridge.
Discussion Character
- Exploratory, Conceptual clarification, Problem interpretation
Approaches and Questions Raised
- Participants discuss rearranging the circuit and applying relevant equations like Q = C V. There is a focus on the difficulty of using standard methods due to the unique arrangement of capacitors, which are not in simple series or parallel configurations. Questions about the nature of the capacitors' values and their impact on calculations are also raised.
Discussion Status
Some participants have offered equations and suggested approaches, while others express uncertainty about their methods and seek clarification. There is an ongoing exploration of different interpretations of the problem, particularly regarding the implications of having different capacitance values.
Contextual Notes
Participants are navigating constraints related to the complexity of the circuit and the lack of straightforward series or parallel relationships among the capacitors. The discussion includes considerations of whether the capacitors have the same or different capacitances.