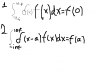Dirac Delta Function Help: Justifying Translation/Sifting Property

[FallenLeibniz]

I have been reviewing some details on the Dirac Delta function and I've hit a
little bit of a road block with trying to wrap my head around how the
Translation/Sifting property of the function is justified. Now according to my
text the overall definition is the generalized function with the "defining
property" that for any continuous function f(x), the integral taken from negativ
e infinity to infinity of the product of f(x) and the D-D function is the value
of f(x) at x=0. (As also shown in eqn 1 of the attached file)

Now a little ways down, the text introduces the "shifted" version of the integral (as shown in eqn 2), and says that through a change of variable to u=x-a, it casts the integral into the form of eqn 1. However, I see no justification
algebraically for this step. Intuitively I see it as just shifting the "focus" of the Dirac-Delta function to pick out f's value at x=a rather than x=0, but am looking to see a formal justification of this. In short basically what I'm wondering is how do I go from having the defining integral as in equation 1 to the integral in equation 2. I would ask for just how the "substitute variable" approach is justified, but if you can provide an explanation that's more rigorous, that would be much appreciated.

Also, I have to apologize. As I am not familiar with Latex, I have resorted to trying to use a paint utility to write out the equations. I have tried my best to represent them, but am no artist.

 

[tiny-tim]

Hi FallenLeibniz!

… I see no justification
algebraically for this step. Intuitively I see it as just shifting the "focus" of the Dirac-Delta function to pick out f's value at x=a rather than x=0, but am looking to see a formal justification of this. … I would ask for just how the "substitute variable" approach is justified, but if you can provide an explanation that's more rigorous, that would be much appreciated.

I don't see the difficulty.

The definition of δ is $\int_{-\infty}^{\infty} \delta(x)f(x)\ dx = f(0)$ for any f

that's the same as $\int_{-\infty}^{\infty} \delta(u)g(u)\ du = g(0)$ for any g and for any variable u

ok, now put u = x - a, du = dx, g(u) = f(u-a) ​

 

[DrewD]

tt,
Did you mean $\int_{-\infty}^{\infty}\delta(u)f(u+a)du$? Or am I getting it backwards in my head?

Also, I have to apologize. As I am not familiar with Latex, I have resorted to trying to use a paint utility to write out the equations. I have tried my best to represent them, but am no artist.

Just learn it. No offense, but your picture was atrocious . Do you run mac, win, or linux? Once you have LaTeX on your computer it will be easier to practice and it will pay off in the long run. I actually make mistakes in emails sometimes because I start typing \infty instead of just saying infinity.

I started with this I think. There is also a LaTeX wikibook that is good, but I don't know if it is easy to use. This site also has a good intro.

 

[WannabeNewton]

Actually, this is a definition of $\delta(x-a)$. Pure formally, it doesn't follow from the substitution rule because $\delta(x-a)$ has never been defined. Clearly, we define it so that the substitution rule is satisfied, but the substitution rule can not be used to proe it. More formally, given a distribution $F$. That means that we have a certain linear functional $F:\mathcal{D}\rightarrow \mathbb{R}$ from the test functions to the real numbers. This is linear and continuous wrt some convergence structure. We often denote F(\varphi) = \int_{-\infty}^{+\infty} F(x)\varphi(x)dx But this is just notation, we don't have an actual integral here in the sense of Riemann or Lebesgue integrals. Given an $a\in \mathbb{R}$, we can define the translation F_a(\varphi) = F(\varphi_{-a}) where $\varphi_{-a}(x) = \varphi(x+a)$. So in our handy integral notation, we have (essentially all equalities are definitions): F_a(\varphi) = \int_{-\infty}^{+\infty} F_a(x)\varphi(x)dx = \int_{-\infty}^{+\infty} F(x-a) \varphi(x) dx and this equals (by definition) F(\varphi_{-a}) = \int_{-\infty}^{+\infty}F(x) \varphi_{-a}(x)dx = \int_{-\infty}^{+\infty} F(x)\varphi(x+a)dx In particular, for the delta function, the following is a definition: \int_{-\infty}^{+\infty}\delta(x-a)\varphi(x)dx = \int_{-\infty}^{+\infty}\delta(x)\varphi(x+a) By definition of the delta function, the latter equals $\varphi(a)$.