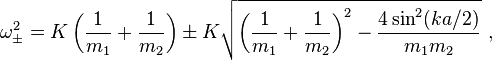SUMMARY
The discussion centers on the dispersion relation for a diatomic linear chain, specifically addressing the behavior when both atoms are set to equal mass (m_1 = m_2 = m). The key issue raised is the persistence of the optical mode term (ω_+) in the dispersion relation, which complicates the reduction to the acoustic mode. The derived equations show that both modes exist due to the two-atom basis, and the confusion arises from the interpretation of the lattice structure. The conversation concludes that the presence of two modes is valid and relates to the choice of reduced versus extended zone schemes.
PREREQUISITES
- Understanding of phonon dispersion relations
- Familiarity with diatomic linear chains in solid-state physics
- Knowledge of trigonometric equations
- Concept of reduced and extended zone schemes
NEXT STEPS
- Study the derivation of phonon dispersion relations in diatomic lattices
- Explore the implications of reduced and extended zone schemes in solid-state physics
- Investigate the physical significance of acoustic and optical modes in crystal structures
- Learn about the mathematical treatment of lattice vibrations and their modes
USEFUL FOR
Physicists, materials scientists, and students studying solid-state physics, particularly those interested in lattice dynamics and phonon behavior in crystal structures.