I Do Electric field lines propagate by themselves away from a charge?

[gionole]

TL;DR

Whether or not electric field lines also propagate and what roles they play in kink formation.

I'm trying to understand how kink would be formed for only electric field for now. Let me share my pictorial understanding. Here is the Link. Moderator's note: The use of external image servers is not allowed. Please upload all images to PhysicsForums.


Note that I'm not looking for math(maxwell equations) discussion, but some logical sense or either just saying what's correct and incorrect about my assumptions below.

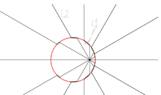
The situation is the following. we start to observe charge shown on the picture from the moment it had already started moving. From some distance to `x1`, charge was moving to constant speed and because of this, we know electric fields just follow the charge direction with the same speed. So far so good. Though, from x1 to x2, charge got accelerated(for our case, it doesn't matter how that happened) which means its speed increased.

For better understanding, let's say while charge was at x1, it had electric field lines in some specific direction(in this case, y) numbered such as 1,2,3,4,5. So these lines kind of move with the same speed to the charge's direction(no kinks formed), but when it was accelerated till x2, you can see how I drew it. Due to acceleration, charge got moved faster, but due to quick acceleration, charge wasn't able to spread this information instantly. So 1,2,3,4,5 still moving with old speed, hence they didn't reach the same `x2` position as charge itself. So at x2, 6 and 7 field lines(new ones) got emitted. So far so good.

What I'm now most interested in is whether 1,2,3,4,5 do also move in the `y` direction(from my picture, they do so) and the picture for my makes sense, but this led me to then ask whether electric field kind of move outwards always as in charge emits new lines which move outwards and then again emits new lines which also move outwards and so on. These thoughts made me got curious whether if my picture about 1,2,3,4,5 moving outwards while they also move to the charge direction is correct, then electric field itself should have some propagation speed, but when I asked this, I kind got an answer that we don't care since we can't create a new charge and observe its propagation. We got charges in the universe which already have electric field around it.

So again, I'm asking whether 1,2,3,4,5 would move in y direction or not(note that i've chosen just one specific direction which I call `y` but ofc I know it's sphere direction all around it) and whether my picture is correct.

I'd love to discuss this. I'd appreciate it because it's been quite some time I'm trying to understand this, asked many people, but either they don't know or I can't wrap my head around what's going on.

 

[Dale]

There is no sense in which a part of the E field is labeled and that you can identify a specific part of the E field now and later.

You can talk about changes in the EM field propagating, and those changes propagate at a specific velocity. But a static unchanging E field neither propagates nor has any assignable velocity.

 

[renormalize]

I'm trying to understand how kink would be formed for only electric field for now. Let me share my pictorial understanding. Here is the Link.

Your link doesn't exist. Please place your supporting material directly into this thread.

 

[Dale]

The closest I can think of to what you seem to want is not the field, but the retarded potential in the Lorenz gauge. The retarded potential in the Lorenz gauge at a given location is due to the charge at the retarded time ($t_r=t-r/c$) and no other time.

So in that sense the potentials in the Lorenz gauge behave as you want, rather than the fields. Be aware that this is a gauge-specific behavior, and the potentials do not behave this way in other gauges

 

[gionole]

I have updated my link. Could you take a look again ?

So If static E field never propagates, then when you take a look at the picture, it won't look like that in the sense that I shouldn't have moved 1,2,3,4,5 to the up(in y direction). but in that case new fields lines(6,7) and old field lines(1,2,3,4,5) will be exactly at the same height on the image which means that when 6th field line is created at x2 position(at the time charge reaches it), then 6 and 1 field line have to join which would gives a kink of horizontal line, but I had always thought the kink would be a little bit downhill.

 

[renormalize]

I have updated my link. Could you take a look again ?

Examine this Wolfram Demonstrations Project and see if it answers your question:

 

[gionole]

Examine this Wolfram Demonstrations Project and see if it answers your question:
View attachment 327383View attachment 327384

The thing I am trying to understand is on my image, you all say that 1,2,3,4,5 field lines dont actually move outwards as a propagation. Which means they stay at the same height.

If so, are the 6 and 7 lines newly emitted field lines from x2 position or they were always there long before ? If they were long before, kink gets created between that long before electric field located at x2 and 1th electric field line.

On the link you shared, it is hard to know there. @Dale maybe you get my point.

 

[Dale]

I shouldn't have moved 1,2,3,4,5

It is more that there is no sense in which you can label the field. The labels 1, …, 5 don’t exist at all. So asking if they move is not a physical question.

 

[gionole]

It is more that there is no sense in which you can label the field. The labels 1, …, 5 don’t exist at all. So asking if they move is not a physical question.

well they are electric field lines the same way the drawings about electric field show on the whole internet. If I cant imagine those lines like that, how will I understand the kink formation where and when happens ?

 

[renormalize]

On the link you shared, it is hard to know there.

Did you run the animation at the link? It shows precisely how E-field lines shift and kink after a charge is instantaneously accelerated. Can you re-express your question in terms of the images in that animation, rather than from your drawing?

 

[Dale]

If I cant imagine those lines like that

The lines are fine. The labels don’t exist. You can imagine the lines as you are doing. But the labels 1, …, 5 are not physically meaningful that I know.

The closest I can think of is the retarded potential.

 

[gionole]

The lines are fine. The labels don’t exist. You can imagine the lines as you are doing. But the labels 1, …, 5 are not physically meaningful that I know.

The closest I can think of is the retarded potential.

The reason I label them is for me to explain my point/reasoning to you. Without labeling, I don't know how to pronounce them.("first line, closer line, the line next to closer one?" - you get my point ?) so line 1 is closer, then line 2 comes after this. It's the same concept.

 

[gionole]

Did you run the animation at the link? It shows precisely how E-field lines shift and kink after a charge is instantaneously accelerated. Can you re-express your question in terms of the images in that animation, rather than from your drawing?

Yes, check here.

We got L1 field lines and L2 field lines. The kink starts from the very start, but I couldn't show you the earlier kink as would be hard for us to exactly see the kink there(while it's there). I'm curious whether L1 field lines are newly emitted ones from acceleration position or they're the field lines which already were there long before as in they were here even when charge was stationary somewhere else.

 

[Dale]

The reason I label them is for me to explain my point/reasoning to you. Without labeling, I don't know how to pronounce them.("first line, closer line, the line next to closer one?" - you get my point ?) so line 1 is closer, then line 2 comes after this. It's the same concept.

I understand. That concept that is unphysical, at least as far as I know.

Changes in the field move. The field itself does not.

The only thing I can think of which behaves the way you want is the retarded potential, not the fields.

 

[renormalize]

I'm curious whether L1 field lines are newly emitted ones from acceleration position or they're the field lines which already were there long before as in they were here even when charge was stationary somewhere else.

E-field lines cannot be "newly emitted", they are ever-present around the charge and extend from the charge to infinity or to other charges of the opposite sign. Note that in the animation, there are exactly 12 lines shown both before and after the impulsive acceleration. They are the same lines.

 

[gionole]

E-field lines cannot be "newly emitted", they are ever-present around the charge and extend from the charge to infinity or to other charges of the opposite sign. Note that in the animation, there are exactly 12 lines shown both before and after the impulsive acceleration. They are the same lines.

If you observe L2 and L1 from the very beginning(exactly when acceleration happened right at that second). On your animation time = 10.1 (would be good to see time = 10.01) but doesn't let me. So at that time, what I'm curious is L2(the whole line) must have moved with old the v2/c speed. I say whole line, because on t=10.1, I get a feeling that L2 is not whole line and near part of charge is cut off which is the whole confusion reason. If you look at it with t=10.1, you will realize. That's why I wanna see the exact acceleration point, because at that acceleration point, L2 must be coming from the charge's old position and it should be the whole line(by whole line I mean, it MUST be coming EXACTLY from old position, shouldn't be cut off). Do you agree? If agree, then let me continue.

Here, I've uploaded the new image

Charge got accelerated from x1 to x2, before it was moving with constant speed. You can see that L1,L2,L3,L4 continued moving with old speed so they are kind of "drawn" from some position which is less than charge's current position.(I labeled them for you to see as L1 = L5, L2 = L6, L3 = L7, L4=L8). Note that L5, L6,L7,L8 completely EXACTLY come from some position(they're not cut off). What I'm now trying to see is which vector gets connected to L5 as a kink and thats what I can't determine.

 

[A.T.]

That's why I wanna see the exact acceleration point,

Here is an interactive simulation, but you would need to install flash player:
https://phet.colorado.edu/en/simulations/radiating-charge

Here is some animations:
http://www.tapir.caltech.edu/~teviet/Waves/empulse.html

 

[gionole]

Here is an interactive simulation, but you would need to install flash player:
https://phet.colorado.edu/en/simulations/radiating-charge

Here is some animations:
http://www.tapir.caltech.edu/~teviet/Waves/empulse.html

How did you install it ? flash player is dead and can't download/install.

 

[A.T.]

How did you install it ? flash player is dead and can't download/install.

I know and it is a pity, because many great educational apps were done with it.

I currently don't have it installed either, and modern bowers won't let you do it. You either have to find a stand-alone player or an old browser with plugin.

 

[A.T.]

That's why I wanna see the exact acceleration point,

The instantaneous acceleration of the charge from one constant speed to another is not really physical. It's assumed in order to simplify the construction of the field line, but I would not read too much into that exact shape of the that kink. With more realistic acceleration it looks smoother.

 

[A.T.]

So again, I'm asking whether 1,2,3,4,5 would move in y direction or not(note that i've chosen just one specific direction which I call `y` but ofc I know it's sphere direction all around it) and whether my picture is correct.

What is moving along y is the information about the x-velocity of the charge and thus the x-velocity the field lines should have.

Your numbers are confusing, but one might try to use such numbers to express how old the information about the state of the charge is at different points along a field line.

 

[vanhees71]

With some sense you can decompose the field of a moving charge into a "self-field" which is dragged along with the charge and the "radiation field", which transports energy and momentum away. Of course, the field is always given by the retarded solution of the Maxwell equations, and this is independent of the choice of gauge, upon which the potentials of course depend, as it should be.

 

[gionole]

What is moving along y is the information about the x-velocity of the charge and thus the x-velocity the field lines should have.

Your numbers are confusing, but one might try to use such numbers to express how old the information about the state of the charge is at different points along a field line.

To simplify the idea, let's look at the picture.

charge till x1 was moving with constant speed, but from x1 to x2, it got accelerated.

Question 1: which one would be kink created from the very beginning - kink 1 or kink 2?
Question 2: If charge was moving with constant speed of `c1` and got quickly accelerated and now moves with `c2` where `c2>c1`, then as far as i understand in the acceleration process when kink was produced, while it moves outwards with the speed of light, it should also be increasing in size(because the old lines that are far away still move with `c1`(old speed) while new lines now move with `c2` with the charge. Each millisecond, the distance between old lines and new lines increase, hence kink moves outwards and increases in size as well. Correct ?
Question 3: They say that kinks are created because electric field lines can't break(E can't be discontinous). This is very bad explanation in my opinion. Even if kink 1 or kink 2 wouldn't have been created, where exactly would we have a space on my image where E wouldn't be there ? without Kink 1 or kink 2, there still would be E field at all points in space. True that there would be old position's electric field, but still. not sure that kink is created because of this.

 

[Dale]

They say that kinks are created because electric field lines can't break(E can't be discontinous). This is very bad explanation in my opinion

I agree here. The kinks are not anything fundamental. Most EM waves won’t even have kinks, so I think any explanation focused on kinks is a very bad explanation.

Kinks will only be produced if the charge’s acceleration is infinite. I.e. if its velocity goes from one value to another instantly. That isn’t particularly realistic, and it isn’t how nature usually behaves.

 

[gionole]

I agree here. The kinks are not anything fundamental. Most EM waves won’t even have kinks, so I think any explanation focused on kinks is a very bad explanation.

Kinks will only be produced if the charge’s acceleration is infinite. I.e. if its velocity goes from one value to another instantly. That isn’t particularly realistic, and it isn’t how nature usually behaves.

Well, is not that what happens anyway ? Changing velocity from one value to another is always instanteneous so there will be kinks produced each time value changes. Why not ? I understand that kinks produced in real life wont be big but super small but still it will be produced as I said as even if velocity changes from 10m/s to 10.11m/s will be instantenous

 

[A.T.]

I understand that kinks produced in real life wont be big but super small but still it will be produced as I said as even if velocity changes from 10m/s to 10.11m/s will be instantenous

No particle with mass can accelerate from 10m/s to 10.11m/s instantaneously (in zero time).

 

[gionole]

No massive particle can accelerate from 10m/s to 10.11m/s instantaneously (in zero time).

if not from 10 to 10.11, it will be from 10 to 10.01. Acceleration is this. At some point changes velocity from some value to another. For sure, changing velocity means that speed has to change. So changing value from 10 to 10.01 is realistic. Kinks should be produced here too. I get that kink will be super small, but why are you saying it wont be at all produced in realistic cases ?

 

[renormalize]

For sure, changing velocity means that speed has to change. So changing value from 10 to 10.01 is realistic. Kinks should be produced here too. I get that kink will be super small, but why are you saying it wont be at all produced in realistic cases ?

In the limit of an infinite number of infinitesimal kinks, the result is no longer a kink. It's a smooth curve that interpolates between the E-field lines before and after the smooth (non-impulsive) acceleration.

 

[DaveC426913]

The field propagates outward at c. Unless I am mistaken*(see sig line) There is no real-world acceleration that can produce a change in velocity that can come close to that - let alone overwhelm it, thus no real kink is produced.

 

[Dale]

Changing velocity from one value to another is always instanteneous so there will be kinks produced each time value changes. Why not ?

No. Forces are not infinite so accelerations are not infinite. A realistic charge acceleration will have a smooth curve, not a kink.

A kink can be a fine approximation if the acceleration is high and your time resolution is low, but it certainly should not serve as the basis of an explanation about EM. So I am not at all surprised that a “kink based” explanation is deficient in other ways.