Do Time-ordering and Time Integrals commute? Peskin(4.22)(4.31)(4.44)

[George Wu]

TL;DR

In Peskin's QFT textbook, according to the explanation below(4.22), the Time-ordered exponential is just a notation, however in the derivation of (4.31),the Time-ordered exponential seems more than just a notation.

In Peskin P85:

It says the Time-ordered exponential is just a notation，in my understanding, it means
$$\begin{aligned}
&T\left\{ \exp \left[ -i\int_{t_0}^t{d}t^{\prime}H_I\left( t^{\prime} \right) \right] \right\}\\
&\ne T\left\{ 1+(-i)\int_{t_0}^t{d}t_1H_I\left( t_1 \right) +\frac{(-i)^2}{2!}\int_{t_0}^t{d}t_1dt_2H_I\left( t_1 \right) H_I\left( t_2 \right) +\cdots \right\}\\
\end{aligned}$$
However in the derivation of (4.31):

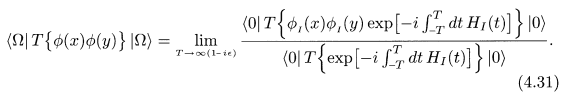
A way to derivate this is: Jens Wagemaker (https://physics.stackexchange.com/users/103623/jens-wagemaker), Why can the time-ordered exponentials be brought to the right?, URL (version: 2023-05-06): https://physics.stackexchange.com/q/762829
Here is his way of derivation:
Note that the time ordering operator is like a sorting algorithm, hence it doesn't matter if we permute something before applying the time ordering operator. In particular we can perform some additional time-ordering by inserting an additional time-ordering operator:
$$\begin{aligned}
A&=T\left\{ \phi _I(x)\phi _I(y)\exp \left[ -i\int_{-T}^T{d}tH_I(t) \right] \right\}\\
&=T\left\{ \phi _I(x)\phi _I(y)T\left\{ \exp \left[ -i\int_{-T}^T{d}tH_I(t) \right] \right\} \right\}\\
&=T\left\{ \phi _I(x)\phi _I(y)U(T,-T) \right\}\\
\end{aligned}$$
We show the case $x_0>y_0$. By 4.26 we get
$$U(T,-T)=U\left(T, x_0\right) U\left(x_0, y_0\right) U\left(y_0,-T\right)$$
which we substitute.
$$A=T\left\{ \phi _I(x)\phi _I(y)U\left( T,x_0 \right) U\left( x_0,y_0 \right) U\left( y_0,-T \right) \right\} $$
Now we want to apply the time ordering. For this we note that the $U\left(T, x_0\right)$ contains only operators with the with in the interval $\left[T, x_0\right]$, and similar for the terms $U\left(x_0, y_0\right)$ and$U\left(y_0,-T\right)$. Hence, if we apply the time ordering we get.
$A=U\left(T, x_0\right) \phi_I(x) U\left(x_0, y_0\right) \phi_I(y) U\left(y_0,-T\right)$, which occurs in the numerator of your second expression.
This step seems straightforward:
$$\begin{aligned}
A&=T\left\{ \phi _I(x)\phi _I(y)\exp \left[ -i\int_{-T}^T{d}tH_I(t) \right] \right\}\\
&=T\left\{ \phi _I(x)\phi _I(y)T\left\{ \exp \left[ -i\int_{-T}^T{d}tH_I(t) \right] \right\} \right\}\\
\end{aligned}$$
However this means:
$$\begin{aligned}
A&=T\left\{ \phi _I(x)\phi _I(y)\exp \left[ -i\int_{-T}^T{d}tH_I(t) \right] \right\}\\
&=T\left\{ \phi _I(x)\phi _I(y)\left[ 1+(-i)\int_{t_0}^t{d}t_1H_I\left( t_1 \right) +\frac{(-i)^2}{2!}\int_{t_0}^t{d}t_1dt_2H_I\left( t_1 \right) H_I\left( t_2 \right) +\cdots \right] \right\}\\
&=T\left\{ \phi _I(x)\phi _I(y)T\left[ 1+(-i)\int_{t_0}^t{d}t_1H_I\left( t_1 \right) +\frac{(-i)^2}{2!}\int_{t_0}^t{d}t_1dt_2H_I\left( t_1 \right) H_I\left( t_2 \right) +\cdots \right] \right\}\\
&=T\left\{ \phi _I(x)\phi _I(y)\left[ 1+(-i)\int_{t_0}^t{d}t_1H_I\left( t_1 \right) +\frac{(-i)^2}{2!}\int_{t_0}^t{d}t_1dt_2T\left\{ H_I\left( t_1 \right) H_I\left( t_2 \right) \right\} +\cdots \right] \right\}\\
&=T\left\{ \phi _I(x)\phi _I(y)T\left\{ \exp \left[ -i\int_{-T}^T{d}tH_I(t) \right] \right\} \right\}\\
&=T\left\{ \phi _I(x)\phi _I(y)U(T,-T) \right\}\\
\end{aligned}$$
In this process we use:
$$\begin{aligned}
&T\left\{ 1+(-i)\int_{t_0}^t{d}t_1H_I\left( t_1 \right) +\frac{(-i)^2}{2!}\int_{t_0}^t{d}t_1dt_2H_I\left( t_1 \right) H_I\left( t_2 \right) +\cdots \right\}\\
&=1+(-i)\int_{t_0}^t{d}t_1H_I\left( t_1 \right) +\frac{(-i)^2}{2!}\int_{t_0}^t{d}t_1dt_2T\left\{ H_I\left( t_1 \right) H_I\left( t_2 \right) \right\} +\cdots\\
\end{aligned}$$
which means :
$$
T\int_{t_0}^t{d}t_1\cdots dt_nH_I\left( t_1 \right) \cdots H_I\left( t_n \right) =\int_{t_0}^t{d}t_1\cdots dt_nT\left\{ H_I\left( t_1 \right) \cdots H_I\left( t_n \right) \right\} $$
What's more, in the derivation of (4.44):

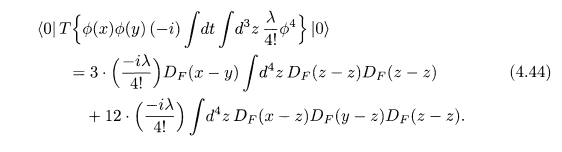
In order to apply wick's theorem, Time-ordering must go inside the integral.
So my question is:
Does Time-ordering and Time Integral commute?
Or in another word:
Can Time-ordering can go inside the integral?

 

[George Wu]

I have found a great answer:
Prahar (https://physics.stackexchange.com/users/8821/prahar), Time ordering of integral, URL (version: 2022-12-17): https://physics.stackexchange.com/q/741494
$$T\int_{t_0}^t{d}t_1\cdots dt_nH_I\left( t_1 \right) \cdots H_I\left( t_n \right)$$
is defined to equal to
$$\int_{t_0}^t{d}t_1\cdots dt_nT\left\{ H_I\left( t_1 \right) \cdots H_I\left( t_n \right) \right\}$$
Otherwise the left side does mean anything.
This definition can be extended to cases like$T\left\{ \phi \left( t\prime_1 \right) \cdots \phi \left( t\prime_m \right) \int_{t_0}^t{d}t_1\cdots dt_n\phi \left( t_1 \right) \cdots \phi \left( t_n \right) \right\}$
$$\begin{aligned}
T\left\{ \phi \left( t\prime_1 \right) \cdots \phi \left( t\prime_m \right) \int_{t_0}^t{d}t_1\cdots dt_n\phi \left( t_1 \right) \cdots \phi \left( t_n \right) \right\} :&=T\left\{ \phi \left( t\prime_1 \right) \cdots \phi \left( t\prime_m \right) \int_{t_0}^t{d}t_1\cdots dt_nT\left\{ \phi \left( t_1 \right) \cdots \phi \left( t_n \right) \right\} \right\}\\
&=\int_{t_0}^t{d}t_1\cdots dt_nT\left\{ \phi \left( t\prime_1 \right) \cdots \phi \left( t\prime_m \right) \phi \left( t_1 \right) \cdots \phi \left( t_n \right) \right\}\\
\end{aligned}$$

 

[Demystifier]

Yes, they commute and it can go inside the integral. Your first inequality should be the equality.

 

[vanhees71]

I think it's a definition of the time-ordering symbol to apply it to the integrand, i.e., to commute it with the integral. It's defined to get a compact notation of the Dyson series of time-dependent perturbation theory in terms of a "time-ordered exponential". If you look at the derivation of this formula, that'll become clear. See, e.g., Sect. 1.9, where it's derived for potential scattering in non-relativistic QM:

https://itp.uni-frankfurt.de/~hees/publ/lect.pdf