You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
What is Peskin: Definition and 115 Discussions
Aaron Dan Peskin (born June 17, 1964) is an American elected official in San Francisco, California. He serves as a member of the San Francisco Board of Supervisors representing Supervisorial District 3, and is currently Dean of the Board. He was elected in 2015, having previously served two terms in 2001–2009.District 3 includes the neighborhoods of North Beach, Chinatown, Telegraph Hill, North Waterfront, Financial District, Nob Hill, Union Square, Maiden Lane, Polk Gulch and part of Russian Hill.
View More On Wikipedia.org
View More On Wikipedia.org
-
M
High Energy Possible typo in Peskin & Schroeder's QFT Textbook (p. 666)?
Hi everyone! I'm going through Peskin & Schroeder's Chapter 19 (Perturbation Theory Anomalies) and it seems to be that equation 19.74 in page 666 has a minus sign missing on the RHS. Namely, I think the correct equation should read \begin{align} (i\not\!\! D)^2 = -D^2 -...- murillo137
- Thread
- Replies: 7
- Forum: Science and Math Textbooks
-

A Do Time-ordering and Time Integrals commute? Peskin(4.22)(4.31)(4.44)
In Peskin P85: It says the Time-ordered exponential is just a notation,in my understanding, it means $$\begin{aligned} &T\left\{ \exp \left[ -i\int_{t_0}^t{d}t^{\prime}H_I\left( t^{\prime} \right) \right] \right\}\\ &\ne T\left\{ 1+(-i)\int_{t_0}^t{d}t_1H_I\left( t_1 \right)... -
T
I Why is there an additional prefactor in equation (12.52) of Peskin's QFT book?
Hey all, I am currently having trouble understanding equation (12.52) in Peskin's QFT book. Specifically the term for external leg corrections, in which they tack on an additional prefactor of ##(-ig)##. Normally with external leg prefactors, we don't see the coupling constant multiplied onto...- thatboi
- Thread
- Replies: 0
- Forum: Quantum Physics
-
T
I Clarification on a Peskin Equation
Hi all, I am currently reading through Peskin's QFT book and have a question regarding an equation that seems very simple in nature: On page 121, below equation (4.121), there is an equation ##(p'-p)^2 = -|\textbf{p}'-\textbf{p}|^2 + \mathcal{O}(\textbf{p}^4)## I was just wondering where exactly...- thatboi
- Thread
-
- Tags
- Peskin
- Replies: 2
- Forum: High Energy, Nuclear, Particle Physics
-

High Energy Another typo in Peskin & Schroeder's QFT?
I'm using a Peskin & Schroeder's copy that looks like it has all typos corrected and I wonder if the following is an undetected typo: On pp. 103 and on the RHS of the bra expression just after (4.68), shouldn't the ##\phi_f({\mathbf p}_f)## be complex conjugated?- apostolosdt
- Thread
- Replies: 1
- Forum: Science and Math Textbooks
-

A Question about S(3) spontaneous symmetry breaking in Peskin & Schroeder
In chapter 20 of Peskin&Schroeder about spontaneous symmetry breaking, he considers and example on page 696 of spontaneous symmetry breaking of SU(3) gauge group with generators taken in adjoint representation. Covariant derivative is defined with: $$D_\mu\phi_a = \partial\phi_a +...- Antarres
- Thread
- Replies: 4
- Forum: High Energy, Nuclear, Particle Physics
-

Weyl Spinors Transformation, QFT1, Peskin, Chapter 3
\begin{align} \psi_L \rightarrow (1-i \vec{\theta} . \frac{{\vec\sigma}}{2} - \vec\beta . \frac{\vec\sigma}{2}) \psi_L \\ \psi_R \rightarrow (1-i \vec{\theta} . \frac{{\vec\sigma}}{2} + \vec\beta . \frac{\vec\sigma}{2}) \psi_R \end{align} I really cannot evaluate these from boost and rotation...- Pouramat
- Thread
- Replies: 12
- Forum: Advanced Physics Homework Help
-

I Ground State in Peskin and Schroeder
In P&S, it is shown that $$e^{-iHT}\ket{0}=e^{-iH_{0}T}\ket{\Omega}\bra{\Omega}\ket{0}+\sum_{n\neq 0}e^{-iE_nT}\ket{n}\bra{n}\ket{0}$$. It is then claimed that by letting $$T\to (\infty(1-i\epsilon)) $$ that the other terms die off much quicker than $$e^{-iE_0T}$$, but my question is why is this...- Diracobama2181
- Thread
- Replies: 7
- Forum: High Energy, Nuclear, Particle Physics
-
N
The meaning of the "physical" electron charge in Peskin (Chap 7)
On p. 246 in the Peskin QFT textbook, below is stated where Z3 is defined as the residue of the q2 = 0 pole, explicitly as $$Z_3=\frac{1}{1-\Pi(0)}$$ and e is the bare charge. In advance, the exact photon two point function is calculated as $$\frac{-ig_{\mu\nu}}{q^2(1-\Pi(q^2))}$$ Though... -

A mathematical derivation in Peskin and Schroeder on page 722.
My attempt at solution is in the HW template, though this is not an HW question.- MathematicalPhysicist
- Thread
- Replies: 1
- Forum: Advanced Physics Homework Help
-
N
Calculation of g-factor correction in Peskin p. 196
I'm reading peskin QFT textbook. In page 196 eq. (6.58) it says $$F_2(q^2=0)=\frac{\alpha}{2\pi}\int ^1_0 dx dy dz \delta (x+y+z-1) \frac{2m^2z(1-z)}{m^2(1-z)^2}\\=\frac{\alpha}{\pi}\int ^1_0 dz\int ^{1-z}_0 dy \frac{z}{1-z}=\frac{\alpha}{2\pi}$$ I confirmed the conversion from the first line...- niss
- Thread
- Replies: 6
- Forum: Advanced Physics Homework Help
-

A A possible mistake in Equations (18.204)-(18.205) in Peskin & Schroeder
They write the following on page 646: Now, equation (17.17) reads: ##\alpha_s(Q) = \frac{2\pi}{b_0 \log(Q/\Lambda)}##, so if I plug ##\alpha_s(Q^2) = \frac{2\pi}{b_0 \log(Q^2/\Lambda)}## into Eq. (18.204) I get: ##\frac{a^f_n}{4b_0}\frac{1}{\log(Q^2/\Lambda)}M^-_{fn}##. Perhaps the...- MathematicalPhysicist
- Thread
- Replies: 5
- Forum: High Energy, Nuclear, Particle Physics
-

A A derivation in Peskin and Schroeder in chapter 18.
They write on page 618: where for those who don't have the book at hand, I'll write the related equations: $$(18.94) \ \ \ \sigma(e^+ e^- \to \text{hadrons})=\frac{4\pi \alpha^2}{s} [ I am c^1(q^2)+Im c^{\bar{q}q}(q^2) \langle 0| m\bar{q}q|0\rangle+ $$ $$+Im c^{F^2}(q^2)\langle 0 |...- MathematicalPhysicist
- Thread
-
- Tags
- Derivation Peskin Schroeder
- Replies: 2
- Forum: High Energy, Nuclear, Particle Physics
-
W
I Cross Section Formula in Peskin and Schroeder
On page 105 of Peskin and Schroeder's book it says that the integral over ##d^2b## in the expression: $$d\sigma = \left(\Pi_f \frac{d^3 p_f}{(2\pi)^3}\frac{1}{2E_f}\right) \int d^2b\left(\Pi_{i=A,B} \int \frac{d^3 k_i}{(2\pi)^3}\frac{\phi_i(k_i)}{\sqrt{2E_i}} \int \frac{d^3...- Wledig
- Thread
- Replies: 8
- Forum: High Energy, Nuclear, Particle Physics
-
G
A Fermion mass terms in Peskin and Schroeder's book
I'm currently looking at how fermion masses are produced via the Higgs mechanism in "An Introduction to Quantum Field Theory" by Peskin and Schroeder. It all makes a lot of sense and I've been fine with it so far, but I ended up getting stuck on something that's driving me nuts. I feel silly... -
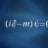
A Smart Algebra of Exp. on Pg 191 of Peskin & Schroeder
Hi all, I have a problem working out the algebra of the following expression in Peskin & Schroeder in a smart way to give the result. It is on page 191, regarding the numerator of the vertex correction function. We want to get from the LHS to the RHS of the following expression...- mdb71
- Thread
- Replies: 3
- Forum: High Energy, Nuclear, Particle Physics
-
M
##CP^N## model in Peskin & Schroeder problem 13.3
My naive attempt to expand the log was##log(k2+A2−λ)=log[(k2−λ)(1+A2(k2−λ))]=log(k2−λ)+log(1+A2(k2−λ))≈log(k2−λ)+A2(k2−λ)##but it did not help me so far since the second term vanishes. Can someone point me to the right direction?- Manu_
- Thread
- Replies: 1
- Forum: Advanced Physics Homework Help
-

I How Peskin & Schroeder simplified this horrible product of bilinears?
P&S had calculated this expression almost explicitly, except that I didn't find a way to exchange the $$\nu \lambda$$ indices, but I'm sure the below identity is used, $$ \begin{aligned}\left(\overline{u}_{1 L} \overline{\sigma}^{\mu} \sigma^{\nu} \overline{\sigma}^{\lambda} u_{2...- hamad12a
- Thread
- Replies: 5
- Forum: Quantum Physics
-

A How does Peskin derive equations 2.51 and 2.52 from equation 2.50 on page 27?
I am trying to verify 2.50 on pg 27 of peskin but did it in my own way, I am sure i made some mistakes here but i was able to get the right answer. Can someone highlight why some of these steps are invalid and explain how peskin git from 2.50 to the first step used in the text for 2.51. And yes...- Rapivcci
- Thread
-
- Tags
- Peskin
- Replies: 2
- Forum: High Energy, Nuclear, Particle Physics
-
W
A Questions from Peskin & Schroeder 5.5 about Compton Scattering
Hi! Just a couple questions on the Compton scattering calculation in P&S. I feel like I'm missing something very simple here but can't quite figure out what it is. On page 166, the amplitude to be evaluated is $$ i\mathcal M = -ie^2 \epsilon_\mu(k)\epsilon^*_\nu(k^\prime) u_R^\dagger(p^\prime)...- Wan
- Thread
- Replies: 1
- Forum: High Energy, Nuclear, Particle Physics
-
L
A Yang-Mills 3 boson Lagrangian term in Peskin and Schroeder
Hi all, I'm not certain if this is the correct section of the forum for this thread but I'm trying to understand ghosts and BRST symmetry and my starting point is chapter 16 of Peskin and Schroeder where I've found a nagging issue. My issue is regarding the derivation of equation (16.6) on...- Liany
- Thread
- Replies: 7
- Forum: High Energy, Nuclear, Particle Physics
-

The superficial degree of divergence in Peskin and Schroeder
Homework Statement I have in the picture attached a screenshot from Peskin's textbook. I don't understand how did they get that for the two last diagrams that ##D=-2##. The question is from pages 316-317 of Peskin's textbook. Homework Equations $$D=4-N_{\gamma}-3/2N_e$$ where ##N_e##=number of...- MathematicalPhysicist
- Thread
-
- Tags
- Degree Divergence Peskin Schroeder
- Replies: 4
- Forum: Advanced Physics Homework Help
-
S
I How to Calculate Page 14 of Peskin Schroeder without Getting Stuck?
Hi Everybody, I am trying to do the calculation of Peskin Schroeder page 14, namely the first block of equations. The author moves from: U(t) = \frac{1}{2 \pi^3} \int d^3p e^{-i(p^2/2m)t} e^{ip \cdot (x-x_0)}. to U(t) = (\frac{m}{2 \pi i t})^{3/2} e^{im(x-x_0)^2/2t}. I guess the way to go...- silverwhale
- Thread
- Replies: 3
- Forum: High Energy, Nuclear, Particle Physics
-

Trouble with Peskin QFT textbook
I'm trying to work through a scattering calculation in the Peskin QFT textbook in chapter 5, specifically getting equation 5.10. They take two bracketed terms 4[p'^{\mu}p^{\nu}+p'^{\nu}p^{\mu}-g^{\mu\nu}(p \cdot p'+m_e^2)] and 4[k_{\mu}k'_{\nu}+k_{\nu}k'_{\mu}-g_{\mu\nu}(k \cdot...- DeathbyGreen
- Thread
- Replies: 1
- Forum: Science and Math Textbooks
-
D
Peskin complex scalar field current
Homework Statement i'm trying to calculate the charge operator for a complex scalar field. I've got the overal problem right but I'm confused about this: On page 18 of Peskin, it is written that the conserved current of a complex scalar field, associated with the transformation ##\phi...- Dansuer
- Thread
- Replies: 1
- Forum: Advanced Physics Homework Help
-
A Charge conjugation in Peskin and Schroeder
Hey there I'm trying to reconstruct the entire table of all Dirac bilinears under C, P, T and CPT transformations of page 71 and hit a wall on charge conjugation. It's a computational problem, really. Here's a specific problem: Equation 3.145 we have $$-i\gamma ^2 \left( \psi ^{\dagger...- diegzumillo
- Thread
- Replies: 4
- Forum: Quantum Physics
-
S
I Two point correlation function in Peskin book
Hello! I am reading Peskin's book on QFT and I reached a part (in chapter 4) where he is analyzing the two-point correlation function for ##\phi^4## theory. At a point he wants to find the evolution in time of ##\phi##, under this Hamiltonian (which is basically the Klein-Gordon - ##H_0## - one...- Silviu
- Thread
- Replies: 11
- Forum: High Energy, Nuclear, Particle Physics
-
S
I Peskin book on QFT question -- 2 integrals for D(x−y)
Hello! Those who used Peskin's book on qft, in chapter 2, Causality (2.4) there are 2 integrals for ##D(x-y)##. Can someone explain to me how does he solve them, as I tried for a bit and didn't manage to do them (actually to get the behavior as ##t \to \infty##). Thank you! -

Differentiation of unitary operator U(t,t') in Peskin and Schroeder
How the authors came to the conclusion (eq. 4.25) that $$ U(t,t')=e^{iH_0(t-t_0)} e^{-iH(t-t')} e^{-iH_0(t'-t_0)} $$- Romanopoulos Stelios
- Thread
- Replies: 5
- Forum: Differential Equations
-

What Explains the Extra Factor of 2 in Peskin and Schroeder's Eq. 18.84?
Homework Statement So I am self-studying the book of Peskin&Schroeder, and there is something I don't understand on page 616. In eq. 18.80, there is a numerical factor of ½ and going from e2 to α will introduce a factor 4π when proceeding to eq. 18.84. But then there should be a numerical...- qqbar
- Thread
- Replies: 1
- Forum: Advanced Physics Homework Help
-

A Peskin Shroeder quantum field 7.31 pag 221
I can't do the derivative 7.31 at page 221. I try to do the derivative dΣ/dpslash, but my result is different from 7.31 Someone can help me writhing the right derivative? Thank you in advance!- dosantos86
- Thread
- Replies: 1
- Forum: Quantum Physics
-

Peskin shroeder quantum field 7.31 pag 221
I can't do the derivative 7.31 at page 221. I try to do the derivative of Σ in dp slash, but my result is different from 7.31 Someone can help me writhing the right derivative? Thank you in advance!- dosantos86
- Thread
- Replies: 1
- Forum: Introductory Physics Homework Help
-
S
Peskin & Schroeder - page 5 - Computation of ##\mathcal{M}##
The following is taken from page 5 of Peskin and Schroeder. It talks about the computation of ##\mathcal{M}## for the annihilation reaction ##e^{+}e^{-}\rightarrow \mu^{+}\mu^{-}##. Even for this simplest of QED processes, the exact expression for ##\mathcal{M}## is not known. Actually this...- spaghetti3451
- Thread
-
- Tags
- Computation Peskin Schroeder
- Replies: 26
- Forum: High Energy, Nuclear, Particle Physics
-
S
Peskin and Schroeder - page 4 - spin and cross section
In chapter 1 of Peskin and Schroeder, the reaction ##e^{+}e^{-}\rightarrow \mu^{+}\mu^{-}## is studied in detail. The related following paragraph is taken from page 4 of Peskin and Schroeder: Both the electron and the muon have spin ##1/2##, so their spin orientations must be specified. It is...- spaghetti3451
- Thread
- Replies: 7
- Forum: High Energy, Nuclear, Particle Physics
-
S
Peskin and Schroeder - page 4 - choice of notation
In page 4, Peskin and Schroeder has the following diagram: The diagram shows the collision of an electron beam and a positron beam to produce a ##\mu^{+}## beam a ##\mu^{-}## beam. My question is this: The electron and positron beams are shown to have momenta ##\textbf{p}## and...- spaghetti3451
- Thread
- Replies: 2
- Forum: Quantum Physics
-
S
How Does the Angular Momentum Commutator Derive the Lorentz Algebra?
In page 39, Peskin and Schroeder write that (3.15) ##{\bf{J}}={\bf{x}} \times{\bf{p}}= {\bf{x}}\times(-i \nabla) ## can be used to derive the Lorentz algebra (3.12) for the rotation group: ##[J^{i},J^{j}] = i \epsilon^{ijk}J^{k}##. I am trying to prove it. Here's my attempt. Can you please...- spaghetti3451
- Thread
- Replies: 3
- Forum: Quantum Physics
-
S
Peskin and Schroeder - Derivation of equation (2.45)
I'm having trouble deriving equation (2.45) on page 25. In particular, in the derivation of ##i\frac{\partial}{\partial t}\pi({\bf{x}},t) = -i(-\nabla^{2}+m^{2}) \phi({\bf{x}},t)##, I need to show that ##\frac{1}{2}\pi({\bf{x}},t) \phi({\bf{x'}},t)(-\nabla^{2}+m^{2}) \phi({\bf{x'}},t) -...- spaghetti3451
- Thread
-
- Tags
- Derivation Peskin Schroeder
- Replies: 2
- Forum: Quantum Physics
-
N
S matrix Unitarity Proof, pg 298 Peskin Schroeder
I have a question regarding a derivation in Peskin and Schroeder's QFT book. On page 298, he is discussing a method for defining a gauge invariant S matrix. He does this by defining projection operators ##P_0## that project general particle states into gauge invariant states, and then defining...- nickodel4
- Thread
- Replies: 1
- Forum: High Energy, Nuclear, Particle Physics
-
R
Contour Integral from Peskin & Schroeder Intro to QFT
1. I'm having some trouble with some of the contour integrals covered in Chapter 2 of Peskin & Schroeder's Intro to QTF. I'm not so much as looking for answers to the integral (in fact, the answers are given in the textbook), but I was hoping someone could point me to some resources to use to...- rolltider
- Thread
- Replies: 10
- Forum: Advanced Physics Homework Help
-
P
Solving Peskin Equation 12.66 Problem
I have a problem with that equation. I understand (dont know if I'm right) that ##p = - M##. But than, isn't ##g\left( { - {{{p^2}} \over {{M^2}}}} \right)## just equal ##g\left( { - 1} \right)##? And my bigest problem: in 12.66 ##\left[ {p{\partial \over {\partial p}} - \beta \left( \lambda...- physichu
- Thread
-
- Tags
- Peskin
- Replies: 4
- Forum: High Energy, Nuclear, Particle Physics
-
N
Cross Section Calc. in Peskin QFT - How to Deal with g^μν.g_μν?
Hello, I'm doing the calculation of the unpolarized cross section in peskin QFT and i am facing a little obstacle, after the calculation of two traces i get terms containing ##g^{\mu \nu}.g_{\mu \nu}## and my question is how to deal with them? does this product equal to a numerical value...- newgate
- Thread
-
- Tags
- Peskin
- Replies: 8
- Forum: Quantum Physics
-

Questions from Peskin and Schroeder
On page 42 of Peskin, at the bottom they say that the next transformation should follow: ##[i\gamma^\mu\partial_\mu - m ]\psi (x) \rightarrow [i\gamma^\mu(\Lambda^{-1})^\nu_\mu \partial_\nu - m ] \Lambda_{1/2} \psi (\Lambda^{-1}x)## But why does the factor ##\Lambda_{1/2}## appear there...- MathematicalPhysicist
- Thread
- Replies: 17
- Forum: High Energy, Nuclear, Particle Physics
-
G
Dimensional Regularization in Peskin
Homework Statement I'm trying to understand dimensional regularization with Peskin. There is a transitions that is not clear. Homework Equations On page 250, the general expression for the d-dimensional integral is given: ##\int \frac{d^d...- gobbles
- Thread
-
- Tags
- Peskin Regularization
- Replies: 2
- Forum: Advanced Physics Homework Help
-
P
How Does Normalization Affect Momentum States in Quantum Mechanics?
What is the value of ##\left\langle {{\bf{p}}|{\bf{p}}} \right\rangle ## when ##a_{\bf{k}}^ + k\left| 0 \right\rangle = \sqrt {2{E_{\bf{p}}}} \left| 0 \right\rangle ##? (like in Peskin) I suppose that ##\left\langle {\bf{k}} \right|{a_{\bf{k}}}{\bf{P}}a_{\bf{k}}^ + \left| {\bf{k}}...- physichu
- Thread
- Replies: 20
- Forum: High Energy, Nuclear, Particle Physics
-
P
Symmetry in Integrals: Peskin's Equation 6.43 & 6.44
In peskin p. 192, they says that the denominator (that is equation 6.43) is symmetric under x<--> y. Thay all so say that you can see it in equation 6.44. But one of the terms in the denominetor is y*q which dose not have that symmetry! Looking at (6.43) and removing the summetric parts leave...- physichu
- Thread
- Replies: 5
- Forum: High Energy, Nuclear, Particle Physics
-
P
Verifying Ward Identity: Need Help With Algebra?
In peskin p. 160 forth paragraph they say to verefy Ward identity in equation 5.74. I don't succeed, they say some algebra is needed. I conjecture that this some algebra is what i miss. Any help will be appreciated - thanks a lot.- physichu
- Thread
- Replies: 2
- Forum: High Energy, Nuclear, Particle Physics
-

Have you conquered Peskin's computation challenges?
Hello everyone,Has anybody already did the computations to reach equations 10.41, 10.44 and 10.45 in Peskin's book? It would be very much appreciated and useful.- Breo
- Thread
-
- Tags
- Computation Doubts Peskin
- Replies: 1
- Forum: High Energy, Nuclear, Particle Physics
-
H
Question on peskin and schroeder
If you go to page 20 and 21 where the Fourier expansion of the klein-gordon field operator is derived, you'll see equation (2.27). Now there are some small details of this whole calculation that I'm confused about. I followed all the way through to (2.25), but here I feel a bit weird. Isn't he...- HomogenousCow
- Thread
- Replies: 1
- Forum: Quantum Physics
-
H
Understanding Peskin Eq 3.50-3.53 and Dirac Spinor
Hi, all I'm reading peskin by myself. I can't understand from eq(3.50) to eq(3.53). i) What should I interpret \sqrt{p\cdot\sigma}? I guess below, but I can't understand \sqrt{\;\;} of matrices. \begin{eqnarray} p\cdot\sigma=E \left(\begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array}\right) -...- h-mina
- Thread
-
- Tags
- Peskin
- Replies: 7
- Forum: Quantum Physics
-
What Is Peskin's Definition of \( j^\mu \) in Noether's Theorem?
Hi all Maybe you could help me understanding this bit from the beginning of the book (peskin - intro to QFT). Homework Statement In section 2.2, subsection "Noether's theorem" he first wants to show that continuous transformations on the fields that leave the equations of motion...- diegzumillo
- Thread
- Replies: 15
- Forum: Advanced Physics Homework Help