Do you know of any software I can use to graph this equation?

[karpmage]

I thought I'd just quickly tell you guys why I want to graph this equation before giving it you.

We're studying conic sections at the moment, and I started wondering what would happen if I let the directrix be a parabola. I looked at the instance where the directrix is y=x^2. I let the focus, F, be (x_F,y_F). Let P=(x,y) be a point on the curve that I am trying to find. I was wondering what the equation of this curve would be if I said that the distance between P and F and the perpendicular distance between P and the directrix has to be the same for any point P. ie. if we let O be the point where P meets the directrix at right angles, then OP=PF. I shall let O=(x_1,y_1)

The gradient of the directrix at point O has to 2(x_1). Thus the gradient of OP has to be (-1/(2(x_1))). Thus, we can represent O as (x+t, y-(t/(2(x_1))), where t is an unknown variable. Since x_1=x+t, we can further represent O as (x+t, y-(t/(2(x+t))). Substituting these values for x_1 and y_1 back into our equation for the directrix, we get:

y-(t/(2(x+t))=(x+t)^2

I let u=x+t, now: y-(u-x)/(2u)=u^2 => 2uy-(u-x)=u^3 => u^3+(1-2y)u-x=0

I then solve this cubic using Cardano's method (method in the link below) http://www.math.cornell.edu/~henderson/courses/M403-S03/cubics.htm

I get u=(((x/2)+((x/2)^2+((1-2y)/3)^3)^0.5)^(1/3))+(((x/2)-((x/2)^2+((1-2y)/3)^3)^0.5)^(1/3)) thus t=(((x/2)+((x/2)^2+((1-2y)/3)^3)^0.5)^(1/3))+(((x/2)-((x/2)^2+((1-2y)/3)^3)^0.5)^(1/3))-x

I want to show that OP=PF. (PF)^2= (x_F-x)^2 + (y_F-y)^2, and (OP)^2 = (y-y_1)^2 + (x-x_1)^2 = (t/(2(x+t))^2 + t^2

Thus, replacing t in terms of x and y we get: (((((x/2)+((x/2)^2+((1-2*y)/3)^3)^0.5)^(1/3))+(((x/2)-((x/2)^2+((1-2*y)/3)^3)^0.5)^(1/3))-x)^2)*((((x/2)+((x/2)^2+((1-2*y)/3)^3)^0.5)^(1/3))+(((x/2)-((x/2)^2+((1-2*y)/3)^3)^0.5)^(1/3))+1)/(4*((((x/2)+((x/2) ^2+(1-2*y)^3)^0.5)^(1/3))+(((x/2)-((x/2)^2+(1-2*y)^3)^0.5)^(1/3)))^2)-(x_F-x)^2-(y_F-y)^2 = 0

(easier to see equation)

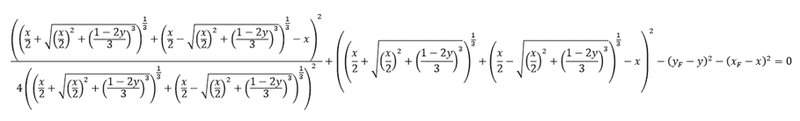
This is the function that I want to plot. I'm just interested to see what it'd look like. Of course I'd have to replace x_F and y_F with set values. I just want to know if any of you know of software which can plot this equation. I don't want to plot a 3-D graph though, unless I am able to set the value of z to 0.

OR

If you guys know of a way to rearrange this equation so that y becomes the subject, then I can simply use any graphing software to plot the curve.

 

[karpmage]

Nevermind, I posted this on another forum and someone answered the question for me. He approached it a little differently, and recommended using mathematica. (Here's a link to his answer)
http://math.stackexchange.com/quest...ange-this-equation/697324?noredirect=1#697324