Discussion Overview
The discussion centers around whether every control system contains an integrator, exploring the nature of control systems, plants, and state-space representations. Participants examine the implications of integrators in control systems and their role in achieving specific system behaviors.
Discussion Character
- Debate/contested
- Conceptual clarification
- Technical explanation
Main Points Raised
- Some participants argue that every plant must consist of an integrator because it converts derivatives back to the variable.
- Others contend that not every control system has an integrator, but many do, as it helps achieve zero DC error.
- One participant suggests that a control system without an integrator operates as a negative feedback system, which has distinct properties.
- Another participant notes that many control systems can function with negative feedback and proportional output without an integrator, citing examples like James Watt's flyball governor.
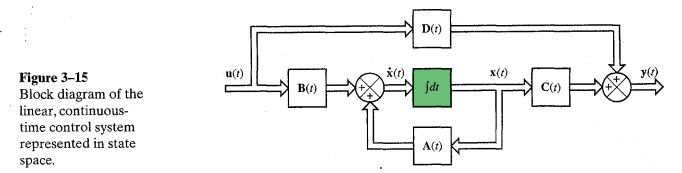
- There is a discussion about the state-space representation, with some asserting that an integrator is inherently part of this representation, while others argue that systems can exist without integrators or derivatives.
- Some participants express that the question may be semantic, emphasizing the need for clear definitions to resolve the discussion.
Areas of Agreement / Disagreement
Participants do not reach a consensus on whether every control system contains an integrator. Multiple competing views remain regarding the role of integrators in control systems and the definitions of plants and state-space representations.
Contextual Notes
Limitations in the discussion include varying definitions of plants and control systems, as well as the potential confusion between the roles of integrators and other components in system design.