sjbauer1215
- 20
- 3
Thank you. I appreciate the work you put in to come up with this answer.
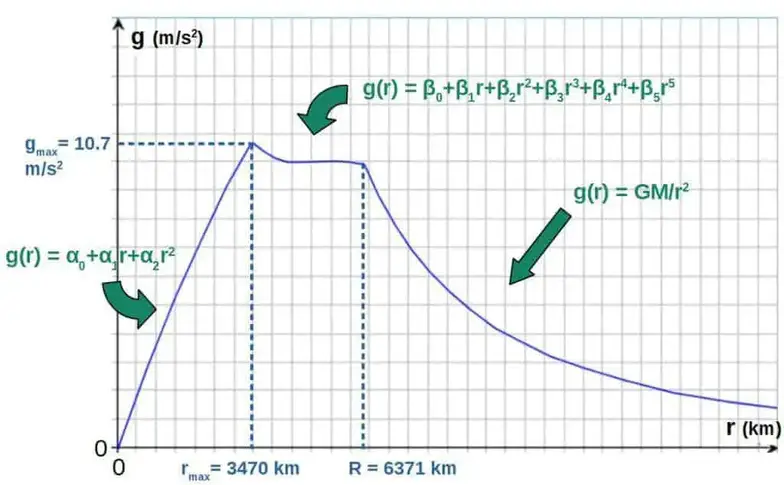
Agreed, but the reduction of field strength inside the inner sphere will always be greater than the reduction of field strength outside of the innermost sphere [i.e. from planet surface to innermost sphere]. So the gravitational rate of acceleration will always be greater inside the innermost sphere even as distance decreases. So over all, in a nonlinear model of stratified layers of increasing density, gravity increases from the planet surface to innermost sphere towards the center of volume as long as there is any distance whatsoever.
Therefore any object near the center of planet will have to deal with increased gravity and pressure, much more so than was encountered on the planet's surface.
Agreed, but the reduction of field strength inside the inner sphere will always be greater than the reduction of field strength outside of the innermost sphere [i.e. from planet surface to innermost sphere]. So the gravitational rate of acceleration will always be greater inside the innermost sphere even as distance decreases. So over all, in a nonlinear model of stratified layers of increasing density, gravity increases from the planet surface to innermost sphere towards the center of volume as long as there is any distance whatsoever.
Therefore any object near the center of planet will have to deal with increased gravity and pressure, much more so than was encountered on the planet's surface.