Undergrad Are Extra Conditions Affecting the Limit Definition?

[Beelzedad]

TL;DR

Do the following extra highlighted words in the $\epsilon-\delta$ definition of limit prevent us from concluding that the limit exists? Why? Why not?

This question consists of two parts: preliminary and the main question. Reading only the main question may be enough to get my point, but if you want details please have a look at the preliminary.

PRELIMINARY:

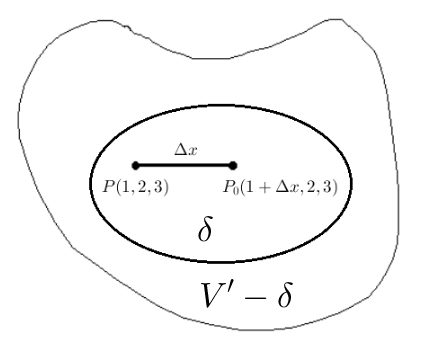
Let potential due to a small volume $\delta$ at a point $(1,2,3)$ inside it be denoted by $\psi_{\delta}$.

_______________________________________________________________________________________________________________________________________________________________________

It can be shown that for every $\epsilon>0$, we can choose a volume $\delta$ such that:

$\left| \dfrac{\psi_{\delta}(1+\Delta x,2,3)-\psi_{\delta}(1,2,3)}{\Delta x} \right| < \dfrac{\epsilon}{3} \tag1$

That is $\epsilon$ can be made as small as we can by choosing a small volume $\delta$.
_______________________________________________________________________________________________________________________________________________________________________

Also, using spherical coordinate system we can show that for every $\epsilon>0$, we can choose a volume $\delta$ such that:

$\displaystyle\left| \iiint_{\delta} \dfrac{\rho'}{R^2} \dfrac{x-x'}{R} dV' \right| < \dfrac{\epsilon}{3}$

That is:

$\displaystyle\left| \iiint_{V'} \dfrac{\rho'}{R^2} \dfrac{x-x'}{R} dV' -\iiint_{(V'-\delta)} \dfrac{\rho'}{R^2} \dfrac{x-x'}{R} dV' \right| < \dfrac{\epsilon}{3} \tag2$

That is $\epsilon$ can be made as small as we can by choosing a small volume $\delta$.
_______________________________________________________________________________________________________________________________________________________________________

No matter what our volume $\delta$ is, at point $P(1,2,3)$, $\dfrac{\partial \psi_{(V'-\delta)}}{\partial x}$ exists (since $P$ being an outside point of $V'−\delta$). That is:

$\lim\limits_{\Delta x \to 0} \dfrac{\psi_{(V'-\delta)}(1+\Delta x,2,3)-\psi_{(V'-\delta)}(1,2,3)}{\Delta x}=\dfrac{\partial \psi_{(V'-\delta)}}{\partial x} (1,2,3)$

That is, for every $\epsilon>0$, we can choose an interval $\delta x$ around $\Delta x=0$ (inside volume $\delta$) such that whenever $0<|\Delta x−0|<\delta x$:

$\left| \dfrac{\psi_{(V'-\delta)}(1+\Delta x,2,3)-\psi_{(V'-\delta)}(1,2,3)}{\Delta x} - \dfrac{\partial \psi_{(V'-\delta)}}{\partial x} (1,2,3) \right| < \dfrac{\epsilon}{3}$

That is:
$\left| \dfrac{\psi_{(V'-\delta)}(1+\Delta x,2,3)-\psi_{(V'-\delta)}(1,2,3)}{\Delta x} - \left( -\displaystyle\iiint_{(V'-\delta)} \dfrac{\rho'}{R^2} \dfrac{x-x'}{R} dV' \right) \right| < \dfrac{\epsilon}{3} \tag3$

That is $\epsilon$ can be made as small as we can by choosing a small interval $\delta x$ around $\Delta x=0$ (inside volume $\delta$)
_______________________________________________________________________________________________________________________________________________________________________

Adding inequalities (1),(2)and (3):

$\left| \dfrac{\psi_{V'}(1+\Delta x,2,3)-\psi_{V'}(1,2,3)}{\Delta x} - \left( -\displaystyle \iiint_{V'} \dfrac{\rho'}{R^2} \dfrac{x-x'}{R} dV' \right) \right| < \epsilon$

That is, for every $\epsilon>0$, we can choose $\bbox[yellow]{\text{a volume δ and}}$ an interval $\delta x$ around $\Delta x=0$ (inside volume $\delta$) such that whenever $0<|\Delta x−0|<\delta x$, the above inequality holds.

That is, $\epsilon$ can be made as small as we can by choosing $\bbox[yellow]{\text{a volume δ and}}$ a small interval $\delta x$ around $\Delta x=0$ (inside volume $\delta$)

QUESTION:

Since there are some extra highlighted words in the above $\epsilon-\delta$ definition of limit, will this prevent us from saying that:

$\lim\limits_{\Delta x \to 0} \dfrac{\psi_{V'}(1+\Delta x,2,3)-\psi_{V'}(1,2,3)}{\Delta x}=-\displaystyle \iiint_{V'} \dfrac{\rho'}{R^2} \dfrac{x-x'}{R} dV'$

? Why? Why not?

 

[Mark44]

Since there are some extra highlighted words in the above $\epsilon-\delta$ definition of limit, will this prevent us from saying that:
$\lim\limits_{\Delta x \to 0} \dfrac{\psi_{V'}(1+\Delta x,2,3)-\psi_{V'}(1,2,3)}{\Delta x}=-\displaystyle \iiint_{V'} \dfrac{\rho'}{R^2} \dfrac{x-x'}{R} dV'$

This seems to be a reasonable conclusion to me.
However, the author's choice of $\delta$ to represent a volume seems very ill-chosen to me, as well as $\delta x$ for an interval around $\Delta x = 0$.