Is Leibniz integral rule allowed in this potential improper integral?

[Beelzedad]

Electric potential at a point inside the charge distribution is:

$\displaystyle \psi (\mathbf{r})=\lim\limits_{\delta \to 0} \int_{V'-\delta} \dfrac{\rho (\mathbf{r'})}{|\mathbf{r}-\mathbf{r'}|} dV'$

where:

$\delta$ is a small volume around point $\mathbf{r}=\mathbf{r'}$
$\mathbf{r}$ is coordinates of field point
$\mathbf{r'}$ is coordinates of source point
$\rho (\mathbf{r'})$ is the density of charge distribution

Taking the gradient of potential:

$\displaystyle \nabla \psi (\mathbf{r}) =\nabla\ \left[ \lim\limits_{\delta \to 0} \int_{V'-\delta} \dfrac{\rho (\mathbf{r'})}{|\mathbf{r}-\mathbf{r'}|} dV' \right] =\lim\limits_{\delta \to 0} \int_{V'-\delta} \rho (\mathbf{r'})\ \nabla \left( \dfrac{1}{|\mathbf{r}-\mathbf{r'}|} \right) dV'$

In the last step, we have applied Leibniz integral rule (basic form).

The validity of this technique for improper integrals is discussed below:

The following passage from the book "Foundations of Potential Theory page 151" says the technique is not valid. But it says the equation $\mathbf{E}=-\nabla \psi$ still holds at points inside source regions $V'$. It also gives a "little" proof of the argument.

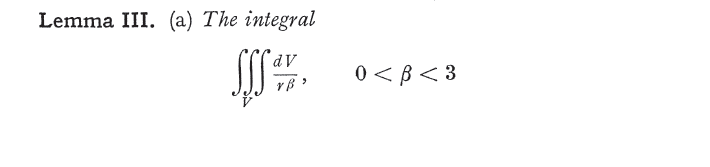
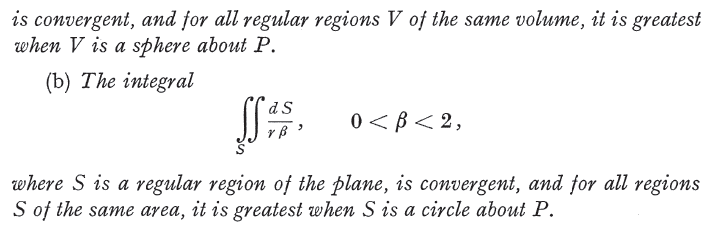
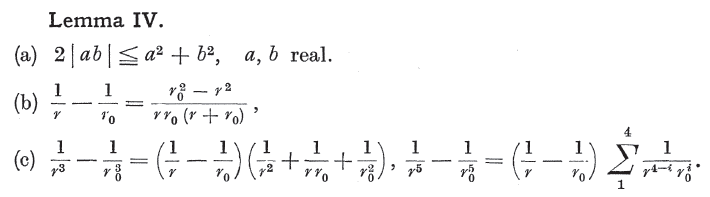
(continued below)

 

[Beelzedad]

Proof:

Unfortunately I am not well versed in potential theory to understand this little proof that the book offers. Can anybody explain the proof in a way in which a Physics graduating student can understand?