Double integral domain with absolute value

[DottZakapa]

Homework Statement

compute the double integral

Relevant Equations

double integral

D={(x,y)∈ℝ²: 2|y|-2≤|x|≤½|y|+1}

I am struggling on finding the domain of such function
my attempt :

first system
\begin{cases}
x≥2y-2\\
-x≥2y-2\\
x≥-2y-2\\
-x≥-2y-2
\end{cases}

second system
\begin{cases}
x≤y/2+1\\
x≤-y/2+1\\
-x≤y/2+1\\
-x≤-y/2+1\\
\end{cases}

i draw the graph and get the intersection for each system, then intersect the two graphs?
first system

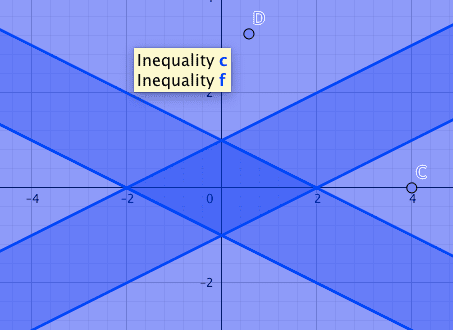
Second

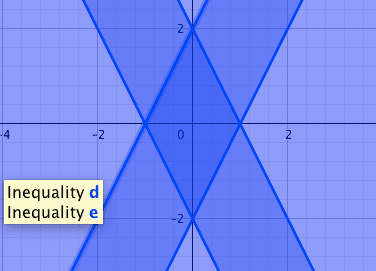
intersection between the two

is the procedure correct or in what am i doing wrong?

 

[PeroK]

Perhaps focus on getting the domain for $y$ first?

 

[HallsofIvy]

It looks to me like you have the second constraint graphed wrong. x= 2|y|- 2 consists of two straight lines, the first, for y\ge 0, x= 2y- 2, is the line through (-2, 0) and (0, 1), the second, for y\le 0, x= -2y- 2, is the line through (-2, 0) and (0, -1). That you appear to have graphed correctly.

But x= (1/2)|y|+ 1 seems to be graphed incorrectly. For y\ge 0 that is x= y/2+ 1 which is a straight line through (2, 2) and (1, 0). For y\le 0 it is x= -y/2+ 1 which is a straight line through (2, -2) and (1, 0).

The region bounded by those is an "arrow head" shaped region pointing to the left. The best way to integrate over that region is probably to divide it into y\ge 0 and y\le 0. For y\ge 0, take y going from 0 to 2 and, for each y, x going from 2y- 2 to y/2+ 1. For y \le 0, take y going from -2 to 0 and, for each y, x going from -2y- 2 to -y/2+ 1.

 

[DottZakapa]

Perhaps focus on getting the domain for $y$ first?

the graph's that you see are depicting each inequality

It looks to me like you have the second constraint graphed wrong. x= 2|y|- 2 consists of two straight lines, the first, for y\ge 0, x= 2y- 2, is the line through (-2, 0) and (0, 1), the second, for y\le 0, x= -2y- 2, is the line through (-2, 0) and (0, -1). That you appear to have graphed correctly.

But x= (1/2)|y|+ 1 seems to be graphed incorrectly. For y\ge 0 that is x= y/2+ 1 which is a straight line through (2, 2) and (1, 0). For y\le 0 it is x= -y/2+ 1 which is a straight line through (2, -2) and (1, 0).

The region bounded by those is an "arrow head" shaped region pointing to the left. The best way to integrate over that region is probably to divide it into y\ge 0 and y\le 0. For y\ge 0, take y going from 0 to 2 and, for each y, x going from 2y- 2 to y/2+ 1. For y \le 0, take y going from -2 to 0 and, for each y, x going from -2y- 2 to -y/2+ 1.

i've just copied and pasted the inequalities of the systems that you see in geogebra, the first mage is of the first system, the second image is related to the second system, the third is merging the two.

Are the two systems correct? in terms of inequalities combinations
the first one is studying the left side of the inequality , the second the right side. Is this the right way to study that domain?

 

[PeroK]

Okay, but you should be able to get $|y| \le 2$ to start things off.