eprparadox
- 133
- 2
Homework Statement
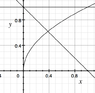
Find the volume under the surface z = y(x+2) and over the area bounded by y+x = 1, y = 1 and y = sqrt(x)
Homework Equations
The Attempt at a Solution
Based on the geometry of the bounds, I broke this integral into two parts. I first found the intersection of the sqrt(x) and y = 1-x. This is at x = \dfrac {1} {2}\left( 3-\sqrt {5}\right)
Then my first integral was this:
\int _{x=0}^{x=\dfrac {1} {2}\left( 3-\sqrt {5}\right) }\int _{y=1-x}^{y=1}y\left( x+2\right) dydx
and my second integral is this:
\int _{x=\dfrac {1} {2}\left( 3-\sqrt {5}\right) }^{x=1}\int _{y=\sqrt {x}}^{y=1}y\left( x+2\right) dydx
However when I solve this integral, I don't get the correct answer (which should be 9/8 according to the solution).
Where am I going wrong?
Thanks!