- #1
dalarev
- 99
- 0
[SOLVED] Double Integration, finding Area
Find: [tex]\int[/tex][tex]\int_{A} xdxdy[/tex] , where A is the area between [tex]y=x^2[/tex] and [tex]y=2x+8[/tex]
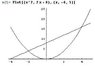
The points of intersection of the two functions is at [tex]x=-2[/tex] and at [tex]x=4[/tex]. Attached is a plot with the area asked to find.
I'm seeing a problem with the x limits of integration changing at x=-2, one of their intersections. I am pretty sure this can be done by summing the 2 areas separately, but the problem asks to solve for the double integral.
Homework Statement
Find: [tex]\int[/tex][tex]\int_{A} xdxdy[/tex] , where A is the area between [tex]y=x^2[/tex] and [tex]y=2x+8[/tex]
Homework Equations
The points of intersection of the two functions is at [tex]x=-2[/tex] and at [tex]x=4[/tex]. Attached is a plot with the area asked to find.
The Attempt at a Solution
I'm seeing a problem with the x limits of integration changing at x=-2, one of their intersections. I am pretty sure this can be done by summing the 2 areas separately, but the problem asks to solve for the double integral.
Attachments
Last edited: