David Charles
- 9
- 1
- TL;DR
- Follow-up to my previous post (Double Slit Interference Question) I have a question regarding the effect(s) of obtaining the which-path information of photons that have travelled through a double slit. I'm posting the question anew without my previous diagram which was incomplete/confusing. The basic question is: if detectors are positioned such that every single photon striking a detector must have come from one or another of the two slits, will this automatically destroy all interference?
A stream of photons pass through a double-slit. The photon stream emerging from each slit then passes through a crystal which splits each photon into coherent entangled pairs. One photon from each pair heads towards a detector (D0) that "can be scanned by a step motor along its x-axis for the observation of interference fringes" and the entangled twin travels toward one of two detectors (one for each slit)
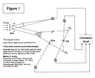
Figure 1 is a replica of a figure from "A DELAYED CHOICE QUANTUM ERASER" - https://arxiv.org/abs/quant-ph/9903047v1. Since many of you are more familiar with this experiment than myself, I won’t explain anything here.
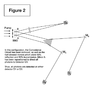
Figure 2 shows a simplified version of the configuration in Figure 1. In Figure 2, the Coincidence Counter has been removed, as well as the half-silvered mirrors. Mirror 3 has been repositioned such that it directs all photons to a detector. All photons will thus be detected at either D1 or D3.
Question: Will the experiment shown in Figure 2 work? (i.e. will the detection of photons at D1 and D3 destroy any interference that may have occurred at D0?)
I'm thinking that in the Figure 2 configuration, the Coincidence Counter is not necessary, as we are not trying to extract a subset of photons from a superset consisting of a mix of photons that had either the which-path information obtained or not.
Thanks, so much.
Figure 1 is a replica of a figure from "A DELAYED CHOICE QUANTUM ERASER" - https://arxiv.org/abs/quant-ph/9903047v1. Since many of you are more familiar with this experiment than myself, I won’t explain anything here.
Figure 2 shows a simplified version of the configuration in Figure 1. In Figure 2, the Coincidence Counter has been removed, as well as the half-silvered mirrors. Mirror 3 has been repositioned such that it directs all photons to a detector. All photons will thus be detected at either D1 or D3.
Question: Will the experiment shown in Figure 2 work? (i.e. will the detection of photons at D1 and D3 destroy any interference that may have occurred at D0?)
I'm thinking that in the Figure 2 configuration, the Coincidence Counter is not necessary, as we are not trying to extract a subset of photons from a superset consisting of a mix of photons that had either the which-path information obtained or not.
Thanks, so much.