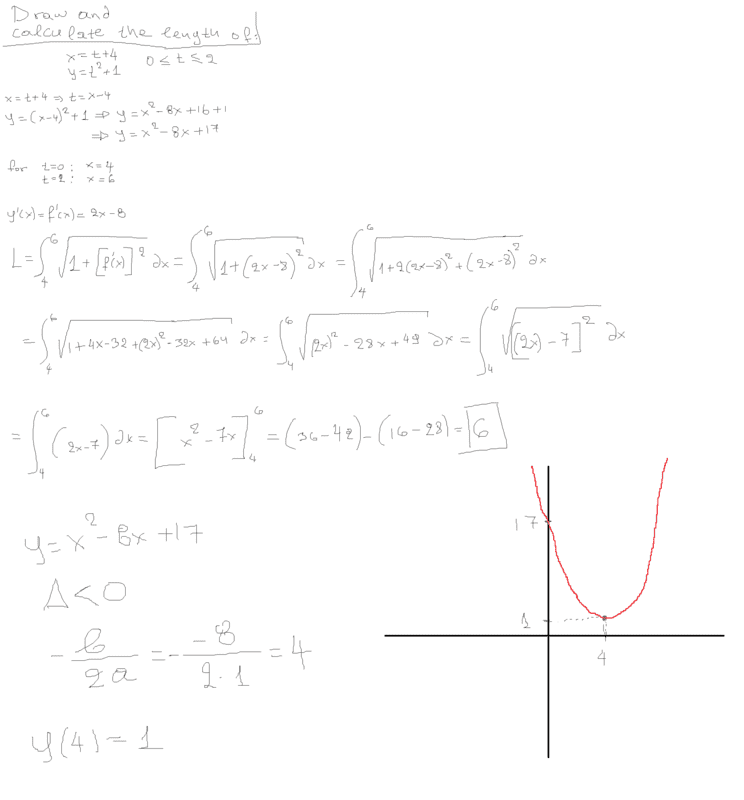SUMMARY
The discussion focuses on calculating the length of the parametric equations x=t+4 and y=t²+1. Participants explore various methods, including setting (2x-8) = sinh(u) and using the parameterization ds² = dx² + dy². The final calculation yields an approximate length of 4.65 using trigonometric functions and inverse hyperbolic sine. The conversation emphasizes the importance of correct parameterization and integration techniques in solving such problems.
PREREQUISITES
- Understanding of parametric equations
- Knowledge of calculus, specifically integration techniques
- Familiarity with hyperbolic functions
- Ability to manipulate and differentiate functions
NEXT STEPS
- Study the derivation of arc length for parametric curves
- Learn about hyperbolic functions and their applications
- Explore Wolfram Alpha for advanced calculus problems
- Investigate the use of parameterization in different contexts
USEFUL FOR
Students and educators in calculus, mathematicians interested in parametric equations, and anyone looking to enhance their understanding of integration and arc length calculations.