- #1
athrun200
- 277
- 0
I had a tutorial today and my tutor said these questions are very trivial so we can simply look at it at home.
But after going home, I found that I don't know how to do Q 35.
I know that p<3 is responsible for the big sphere with r=3. But I don't know why the other part is responsible for the small sphere
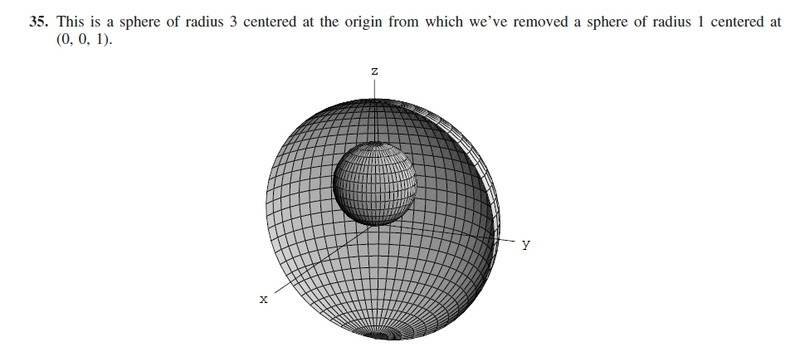
But after going home, I found that I don't know how to do Q 35.
I know that p<3 is responsible for the big sphere with r=3. But I don't know why the other part is responsible for the small sphere