Drawing Radial Field Equipotentials and Field Lines

[AN630078]

Homework Statement

Hello, I have a question asking me to draw a radial gravitational field showing the gravitational field lines and the equipotential surfaces for equal energy increments. I then have to comment upon the spacing of the field lines and equipotential lines.

My query is in this question would it be referring to the spacing visually when drawing the field lines and equipotentials or what this spacing represents in a radial field?

I am not sure how to comprehensively answer what is being asked and would be very grateful for any advice

Relevant Equations

g=GM/r^2

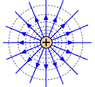
I have just attached a standard depiction of a radial field as one may similarly choose to draw it. So I understand that the gravitational field strength in a field is defined as the force per unit mass at that point. The field lines in a radial field move further apart further away from the centre indicating the field strength is reducing. The closer together the field lines the stronger the field and thus the force.
The equipotential surfaces of a radial field are positions within a field with zero difference in potential between them; ie. the potential on an equipotential surface is the same everywhere as connected by equipotential lines. The field will always be perpendicular to the equipotential lines; since a field is defined as a region in which potential changes. How close the equipotentials are indicates the strength of the electric field and how quickly the potential is changing. e.g. a stronger field has closer equipotentials.

In a radial field, the field lines are all equally separated in terms of field strength but the radial distance between them increases as you move further from the planet. If this question is just asking how to draw a general radial field with field and equipotential lines then one would say that the field lines are evenly spaced but increase in distance further from the centre? And moreover, would the equipotential surfaces be said visually to be drawn unequally spaced with successive shells representing equal intervals of potential difference.

So for a radial field the field lines are evenly spaced but the equipotential surfaces are unevenly spaced?

Moreover, could an alternative unit for gravitational field strength besides N kg^-1 be Jm^-1kg^-1?

 

[kuruman]

You want equal energy increments so you have to start with the equation for the potential energy per unit mass, $V(r)$ not force per unit mass $g(r)$.
If $V(r)=-\dfrac{GM}{r}$, then $$\Delta V = GM\frac{\Delta r}{r^2}~\Rightarrow ~\frac{\Delta V}{V}=-\frac{\Delta r}{r}.$$Can you devise an iterative plotting procedure that exploits the above condition?

You can devise any alternative unit for gravitational field strength that you want, but m/s² is more conventional and most easily recognizable by everyone.

 

[AN630078]

You want equal energy increments so you have to start with the equation for the potential energy per unit mass, $V(r)$ not force per unit mass $g(r)$.
If $V(r)=-\dfrac{GM}{r}$, then $$\Delta V = GM\frac{\Delta r}{r^2}~\Rightarrow ~\frac{\Delta V}{V}=-\frac{\Delta r}{r}.$$Can you devise an iterative plotting procedure that exploits the above condition?

You can devise any alternative unit for gravitational field strength that you want, but m/s² is more conventional and most easily recognizable by everyone.

Thank you for your reply. I do not know what you mean by an iterative plotting procedure.
In regard to an alternative unit for gravitational field strength, yes thank you for your suggestion I am aware of the use of m/s^2? However, would Jm^-1kg^-1 be a suitable alternative, although lesser used?

 

[kuruman]

Thank you for your reply. I do not know what you mean by an iterative plotting procedure.
In regard to an alternative unit for gravitational field strength, yes thank you for your suggestion I am aware of the use of m/s^2? However, would Jm^-1kg^-1 be a suitable alternative, although lesser used?

Iterative procedure:
Decide on a value for the constant increment $\Delta V$.
Find a number for the potential $V$ at $r = R_E$ (the Earth's radius) and draw an equipotential at that $r$. Label it with the value of $V.$
1. Solve the equation $\dfrac{\Delta V}{V}=-\dfrac{\Delta r}{r}$ to get the magnitude of the radius increment $\Delta r$ and add it to the old $r$. Ignore the negative sign.
2. Add the increment $\Delta V$ to the old potential to get the new $V$ and draw an equipotential at the new $r.$ Label it with the new value of $V.$
3. Go back to step 1 and repeat.

However, would Jm^-1kg^-1 be a suitable alternative, although lesser used?

In my opinion no, for the same reason that one uses Joules and not kg⋅m²/s².