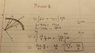- #1
AGGENGR
- 20
- 0
1. Looking to find E-field and Voltage (in pic)
2. Coulomb's Law, E=q0V, E=integralde
3. Basically i tried to split the quarter ring into halves and then integrate. It worked i got the right answer. But my professor did it in 1 step? Something about just integrating over DV? I don't get how or why since when you do E-field integration you have to account for the splitting up of dq into lamdadl, etc like i did (also in a pic).
Also how did she get the same result in Number 2? I got 2 times the result because there are twice as many rings?
2. Coulomb's Law, E=q0V, E=integralde
3. Basically i tried to split the quarter ring into halves and then integrate. It worked i got the right answer. But my professor did it in 1 step? Something about just integrating over DV? I don't get how or why since when you do E-field integration you have to account for the splitting up of dq into lamdadl, etc like i did (also in a pic).
Also how did she get the same result in Number 2? I got 2 times the result because there are twice as many rings?