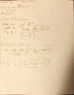E&M Exam Question, I want to know what I did wrong

[ParticleGinger6]

Homework Statement

A dielectric slab, infinite in the xy-plane with dielectric constant epsilon r = 4, is
placed above an infinite perfect conductor as shown. A uniform surface charge
density sigma is placed on the upper surface of the conductor. (Picture in attached file)

a.) Find the electric displacement D and the electric field E inside and above the dielectric.
b.) Determine the polarization P inside the dielectric.
c.) Find the bound charge densities of the dielectric.

Relevant Equations

(in the second attached file)

(the second attached file)

 

[Jody]

I'm having a hard time following your work. Do you know the electric field of a charged infinite sheet?

Did your professor cover boundary conditions? I feel like this question is hinting at it.

The polarization one I was totally baffled and admit I'm very weak on that topic; so: I've grabbed my book and I'm not sure if I'm understanding it right. I don't know if it would be the right approach so I'll put it in spoilers.

Spoiler

Disclaimer: I admit I do not know the answer and do not know if this is an acceptable approach.

$$D = \epsilon_0 E + P$$

Where $P$ is your polarization field. I'm not sure if it would be right to say $D = \epsilon E = \epsilon_r \epsilon_0 E$. If I were in the middle of the exam and had the first equation I'd put that into the left side and solve for $P$.

 

[Delta2]

A bit hard to understand what you doing but let's see.

I suppose you apply Gauss's law in a "proper" closed gaussian surface which's one side (the one parallel to the conducting sheet) has surface XY (is that what XY is about?). Then why XY is mysteriously disappearing in a) when you take the electric field E inside to be $E=\frac{Q}{4\epsilon_0}$. Algebraically is not correct what you do there.
Perhaps you wanted to write $E=\frac{Q}{XY}\frac{1}{4\epsilon_0}=\sigma\frac{1}{4\epsilon_0}$?
But even so i believe the result is wrong and it all starts because you don't apply Gauss's law correctly.

 

[kuruman]

1. From Gauss's law using a pillbox whose one face is inside the conductor and the other inside the dielectric
$D A=\sigma A \rightarrow D=\sigma$.
2. Inside the dielectric you correctly wrote $D=\epsilon_0 E+P$ and $E=\dfrac{D}{\epsilon}$. So, with the result from part 1, $$\sigma=\epsilon_0 \frac{\sigma}{\epsilon}+P~ \rightarrow~P=\sigma\left(1-\frac{\epsilon_0}{\epsilon}\right).$$
3. The surface bound charge density is equal to $P$. Of course $\dfrac{\epsilon_0}{\epsilon}=\dfrac{1}{4}$.

So what did you do wrong? You insisted on using $Q$ for the enclosed charge instead of using the given charge density $\sigma$. Thus, you got stuck with this silly $Q/XY$ that you did not recognize as the surface charge density.