{Edit-Solved} Confirmation requested on deriving functions from graphs

[warhammer]

TL;DR

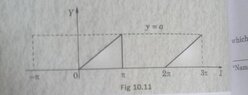
So I basically saw this graph specified as a particular waveform in my book while reading Fourier Series. I decided to try and derive its function since once I do that I can easily find the FS. Please find the photo and my attempt below, just need a small confirmation if I'm right/wrong.

So I thought that the graph tries to tell us that the function is periodic after 2π interval. So I tried to derive its function from the graph as follows using the point slope equation form for the points (0,0) & (a,π): $y= ({a}/{π})*x$

I hope this function is alright and I just need to find its Fourier Series

 

[anuttarasammyak]

Actually the graph shows
$y=\frac{a}{\pi}(x-2n\pi)$ for $0<(x-2n\pi)<\pi$ for integer n
y=0 for others.

 

[warhammer]

Actually the graph shows
$y=\frac{a}{\pi}x$ for $2n\pi<x<(2n+1)\pi$ for integer n
y=0 for others.

Oh I see. Now I realize how you have represented it an even general manner. Although I am a bit confused now, how should I find FS for the same, I mean I'm confused about the intervalbin which integration for FS will be carried out..

 

[anuttarasammyak]

Because the function, say f(x), has period of 2$\pi$, it is expressed as
f(x)=\frac{a_0}{2}+\sum_{k=1}^\infty (b_k \sin kx + a_k \cos kx)
You may calculate $a_k$ and $b_k$ in a usual way.

 

[warhammer]

Because the function, say f(x), has period of 2$\pi$, it is expressed as
f(x)=\frac{a_0}{2}+\sum_{k=1}^\infty (b_k \sin kx + a_k \cos kx)
You may calculate $a_k$ and $b_k$ in a usual way.

Thank you so much! Now I get it