salparadise
- 22
- 0
Hello,
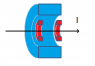
Imagine I have an infinite wire with a DC current. Around it there two rings of ferro-magnetic material, not far from each other.
Does changing the mu_r of one of the first ring, changes the magnetic field in the second ring?
- If I consider just Ampére law (macroscopic formulation), I would say that since H doesn't change by changing the magnetic permeability, then B on the second ring should not change.
- But when I think about the total energy of the system (Em=1/2.B.H). Since in the first ring B increases, the total energy of the system should also increase, which doesn't make sense to me.
This is really troubling me, considering that I should have learned enough of E.M. to know this.
Any lights on this would be very helpful,
Thanks
Imagine I have an infinite wire with a DC current. Around it there two rings of ferro-magnetic material, not far from each other.
Does changing the mu_r of one of the first ring, changes the magnetic field in the second ring?
- If I consider just Ampére law (macroscopic formulation), I would say that since H doesn't change by changing the magnetic permeability, then B on the second ring should not change.
- But when I think about the total energy of the system (Em=1/2.B.H). Since in the first ring B increases, the total energy of the system should also increase, which doesn't make sense to me.
This is really troubling me, considering that I should have learned enough of E.M. to know this.
Any lights on this would be very helpful,
Thanks