Efficiency of a heat engine given a P-V diagram of its process

[XSummer32]

Homework Statement

Hello, I'm attempting a question and I'm not sure what I did wrong with my answer
This is the question:

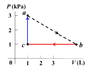
A volume of ideal gas, Cv = 1.21R, undergoes a cyclic process, the triangle abc in the p-V diagram. It starts at point a (T = 300 K, P = 3 kPa, V = 1 L) and expands until the volume reaches 6.3 liter at point b. It then gives away heat to the environment at constant pressure until its volume decreases to point c (P = 1 kPa, V = 1 L). Finally, it absorbs heat at constant volume and gets back to point a. Find the efficiency (%) of this heat engine.

(hint: find the total net work (W) done, and identify the processes (ab and ca) in which the gas absorbs a total amount of heat Qh. The efficiency is then W/Qh.

Relevant Equations

Q - isothermal = nRT ln(v2/v1)
volume constant = nCv * Change in Temperature

Work done - Isothermal = -nRT ln (v2/v1)
Isobaric = -P * Change in volume

Efficiency = W/Qh

I post the working in the attached file

 

[Chestermiller]

I can't read your handwriting; your post is unreadable. Just write out your last two equations using LaTex, and I'll see what you've come up with.