Efficiency of the Rankine Cycle

[TheBigDig]

Homework Statement

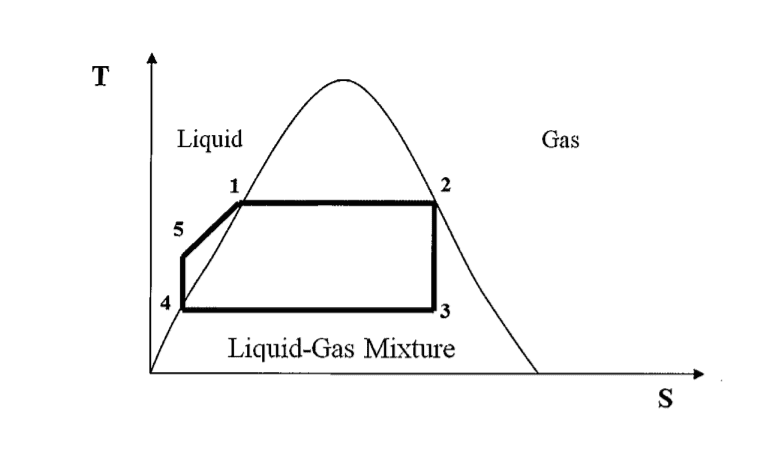
A power plant operates on the Rankine cycle sketched below. The enthalpies at the four states marked 1,2,3 and 4 are:
h1 = 1200 kJ/kg, h2 = 2700kJ/kg, h3 = 1800kJ/kg, h4 = 130kJ/kg
If the overall efficiency of the cycle is 31%, calculate the enthalpy at point 5. Hence calculate the work ratio rw

Relevant Equations

$$\eta = \frac{W_T-W_P}{Q} = \frac{(h_3-h_2)-(h_5-h_4)}{h_4-h_3}$$
$$r_w = \frac{W_T-W_P}{W_T}$$

W_T, the work done by the turbines, as the difference in enthalpy from point 2 to point 3
W_P, the work done by the pumps as the difference in enthalpy from point 4 to point 5
Q as the difference in enthalpy from point 3 to point 4

Taking these I get h₅ = -252.3kJ/kg. However, my work ratio is larger than 1 and negative. Also I'm not entirely sure what a negative enthalpy represents physically.

I was working from this source here: https://www.nuclear-power.net/nucle...y-of-rankine-cycle-equations-and-calculation/

 

[Chestermiller]

Your starting equation is incorrect. It should read:
$$\eta=\frac{(h_2-h_3)-(h_5-h_4)}{(h_2-h_5)}$$The heat added Q is $h_2-h_5$. The heat removed in the condenser is $h_3-h_4$. You also had the wrong sign on the work done by the turbine.

 

[TheBigDig]

Thanks so much! Will try that out asap

 

[Chestermiller]

Thanks so much! Will try that out asap

Good. But do you see where you erred?

 

[TheBigDig]

Good. But do you see where you erred?

Yes, I had been blindly following the source I quoted but when I put a bit of thought into why it was wrong it was obvious.
4-> 5 the water is getting pumped at a high pressure (q = 0)
2->5 is where heat energy is added to the system to raise the temperature at a constant pressure (w = 0)
2->3 is an expansion through the turbine (q = 0)