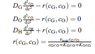MATLAB Efficiently Solving Diffusion-Based Equations Using Shooting Method in MATLAB

[baseball1234]

Hi, I have the attached diffusion based equations I am looking to solve, however I am unsure about how to implement. I have solved similar equations before, with a simplified r(cG,cO) using the explicit finite difference method and it worked fine. However, I am wondering if that would be OK for this set of equations. I read that people used shooting method to solve these, but I am unfamiliar with this method. Can I also use the differential equation solvers in MATLAB to do this? Thanks.

 

[baseball1234]

Hi, I have developed a program in MATLAB to solve these equations, however I was wondering if someone can take a look for me. My solutions are all coming out to be "NaN", which is "not-a-number" in Matlab. I am using the explicit finite difference scheme to solve. Any suggestions would be great. My code below will run in MATLAB from just a copy/paste from here. My boundary conditions are the following:

x = 0: dcG/dx=0, dcO/dx=0 and cH = 0  
x = d: cG = cG0, cO = O20, cH = 0 
 
 Initial conditions are
 
 cH(t = 0) = 0
 cG(t = 0) =cG0
 cO(t = 0) = O20

clear all;

numx =50;                       %number of grid points in space
numt =82000;                    %number of time steps to be iterated over 
tmax = .06;

Length =50E-7;                  %length of grid
DG = 4E-10;                     %requirement DG(dt)/dx^2 < .5, cm^2/sec
DO = 5E-9;                      %requirement DO(dt)/dx^2 < .5, cm^2/sec
DH = 5E-9;                      %requirement DH(dt)/dx^2 < .5, cm^2/sec            

Vmax = 60E-6;                   %A/cm^2
KG = 33E-6;                     %mol/cm^3
KO = .2E-6;
G0 =2E-6;                       %mol/cm^3 initial substrate concentration
O20 = .12E-6;                   %mol/cm^3 inital oxygen concentration

cG = zeros(numx,1);              %initialize everything to zero
cH = zeros(numx,1);              %initialize everything to zero
cO = zeros(numx,1);

zcG = linspace(0,Length,numx)';   %vector of x values, to be used for plotting
tG = linspace(0,tmax,numt)';      %vector of t values, to be used for plotting

zcO = linspace(0,Length,numx)';   %vector of x values, to be used for plotting
tO = linspace(0,tmax,numt)';      %vector of t values, to be used for plotting

zcH = linspace(0,Length,numx)';   %vector of x values, to be used for plotting
tH = linspace(0,tmax,numt)';      %vector of t values, to be used for plotting

dxG = zcG(2)-zcG(1);              %Define grid spacing in time
dtG = tG(2)-tG(1);                %Define grid spacing in time

dxO = zcO(2)-zcO(1);              %Define grid spacing in time
dtO = tO(2)-tO(1);                %Define grid spacing in time

dxH = zcH(2)-zcH(1);              %Define grid spacing in time
dtH = tH(2)-tH(1);                %Define grid spacing in time

S_Stability1 = (DG*dtG)/((dxG)^2) %check requirement DG(dtG)/dxG^2 < .5, cm^2/sec
O_Stability1 = (DO*dtO)/((dxO)^2) %check requirement DO(dtO)/dxO^2 < .5, cm^2/sec
H_Stability1 = (DH*dtH)/((dxH)^2) %check requirement DH(dtH)/dxH^2 < .5
        
%{ 
Dirchelet Boundary Conditions, where Neumann BC dcG/dx=0 and dcO/dx=0
is in body of for loop below, IC is given by matrix initialization (zeros) and BC
%}

cG(numx) = G0;                 %cG(x=d,t)=G0
cO(numx) = O20;                %cO(x=d,t)=O20
cH(1) = 0;                     %cH(x=0,t)=0
cH(numx) = 0;                  %cH(x=d,t)=0

%iterate central difference equation% 

for j=1:numt %time loop  
    
           cGlast = cG;
           cOlast = cO;
           cHlast = cH;
           
      
    for i=2:numx-1 %space loop
              
      cG(i) = cGlast(i) + (dtG/dxG^2)*DG*(cGlast(i+1) - 2*cGlast(i) + cGlast(i-1))-((Vmax*dtG*cGlast(i)*cOlast(i))/(cGlast(i)*cOlast(i)+(KG*cOlast(i))+KO*cGlast(i))); 
      cO(i) = cOlast(i) + (dtO/dxO^2)*DO*(cOlast(i+1) - 2*cOlast(i) + cOlast(i-1))-((Vmax*dtO*cGlast(i)*cOlast(i))/(cGlast(i)*cOlast(i)+(KG*cOlast(i))+KO*cGlast(i)));
      cH(i) = cHlast(i) + (dtH/dxH^2)*DH*(cHlast(i+1) - 2*cHlast(i) + cHlast(i-1))+((Vmax*dtH*cGlast(i)*cOlast(i))/(cGlast(i)*cOlast(i)+(KG*cOlast(i))+KO*cGlast(i)));
      
      y(j,1) = cH(2);  %store data in vector for current plotting 
      
    end
    
    cG(1)= cGlast(1)+dtG*DG*2*(cGlast(2)-cGlast(1))./dxG.^2; %Neumann Boundary Condition
    cO(1)= cOlast(1)+dtO*DO*2*(cOlast(2)-cOlast(1))./dxO.^2; %Neumann Boundary Condition 
    
end

figure(1);
plot(zcH,cH);
xlabel('Length (cm)');
ylabel('[H2O2] (M)');

figure(2);
plot(zcG,cG);
xlabel('Length (cm)');
ylabel('[Glucose] (M)');


figure(3);
plot(zcO,cO);
xlabel('Length (cm)');
ylabel('[O2] (M)');

figure(4);   
i = 2*(96500)*DH*(y/dxH);
%i = 2*(96500)*DH*(y/dxH);
plot(tH,i);
xlabel('Time (s)');
ylabel('Current (A)');