yuiop said:
Hi Austin, sorry for the delay getting back to you on your questions here. ..
Hi yuiop ,,no problem ,,,me too .
yuiop said:
Your equations seem to suggest that the accelerating clocks would agree on on the distances MFM and FMF without any adjustment of the clocks and in fact you obtain MFM=FMF=2D. I see you have used the equation x = (1/2)aT^2, because the time used in that expression is not the elapsed proper time of the accelerating clocks and nor is it the elapsed time of a clock in the CMIRF. It is the time measured by a third coordinate system of an inertial system moving at the average speed of the accelerating clock between two events and in this case, T = sqrt(x^2+t^2) where t is the time measured in the CMIRF that is moving at the instantaneous speed of the accelerating clock. If you have still been following this thread, I hope you will now agree that we have demonstrated that we can come up with a scheme that makes the one way speed of light isotropic.
No actually I thought it was the time measured in the inertial frame where the accelerated system was initially at rest. The frame which is the frame for the diagrams.
Austin0 said:
This raises the question of where the midpoint of the system would be located as determined by simultaneous reception of signals sent in both directions yes?
Assuming that the midpoint was so determined then if the signals are sent from the midpoint and relfected from the front, back to the midpoint and from the midpoint to the back and return it seems like observing inertial frames would agree on this equivalence. So am I incorrect in this conclusion??
yuiop said:
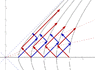
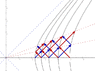
This is easy enough. First we place a clock at an assumed point M. We then place a mirror upstream at a suitable point (F) upstream where the radar signal returns in time t as measured by the clock at M. We place another mirror downstream which is located at a point (B) where the radar signal also returns simultaneously in time t. We can now agree that M is the midpoint between F and B in the accelerating system. This midpoint will not look like it is located midway in the CMIRF and in the CMIRF the distance MB looks shorter than MF and in effect, both distances look length contracted in the CMIRF with the rear section looking more length contracted than the front section.
Yes your easy method was just what I described and the question I posed was based on the understanding that the midpoint so deirived would not be in the middle of the system or the CMIRF.
I think you may be mistaken about MB and MF both appearing contracted to the middle CMIRF.
I thin the back would be contracted and the front would be relatively larger than the local metric or section of the middle CMIRF
If the system is viewed as a composite of 3 CMIRFs the back 1/3 would be contracted and the front 1/3 would be expanded relative to the middle CMIRF yes?
Austin0 said:
If reflected measurements are made from the central point in both directions then distances from that point as derived by (0.5*dt*c) should be equivalent in both directions and one way synchronizations from a continuous synch signal based on those distances should then work throughout the system. The intervals should also be uniform through the system and no special spacing required Yes??
Or am I off here?
yuiop said:
Yes and no. It looks like I have applied special spacing but this would come about naturally due to length contraction.
WHy would length contraction be relevant if using calibrated clocks [all running same rate] and synchronization from a central master clock?
Wouldn't lengths derived from such clocks be equivalent throughout the system?
Austin0 said:
If this is at alll accurate this setup would then be equivalent to the CMIRF centered on the system.
WIth continued agreement between this system and successive CMIRFs if calibration is based on a continuous synch signal or equivalent computaitonal clock adjustment.
But there would not be agreement with local natural rulers.
yuiop said:
Actually, there would be agreement with local natural rulers. Let us say we have a long rocket that is moving inertially and has a series of rulers layed end to end that are all the same length and in agreement with the radar distances measured inertially by clocks placed at the end of each ruler. If the rocket now transfers from inertial motion to accelerating motion to Born rigid accelerating motion the rulers will length contract (more so at the back) and have the "special spacing" that I depicted in the second diagram I uploaded earlier. The length contraction of the rulers is natural. THe adjustment to the clocks to get the radar measurements to agree with the ruler lengths isotropically is artificaial, but can be done.
Using the analogy of the back CMIRF wouldn't the local clock radar measurements agree with the ruler measurements if it is in fact equivalent to a locally instantaneous inertial frame? It would only be with radar measurements over greater distances in the system that the natural dilation of the rear clock would not agree with distance or am I missing again?
Austin0 said:
If there was a long ruler running the length of the system and this ruler was naturally Born accelerate, then indicated intervals would be shorter at the back and longer at the front, relative to the artificially calibrated ruler lengths derived from the light synch and calibration of the quasi-inertial coordinate frame. Ruler lengths derived from naturally dilated clocks at the back would also seem to mean a shorter length in comparison with the artificailly derived length , would you agree?
yuiop said:
As above, natural ruler lengths would be in agreement with "quasi-inertial coordinate" calibrated rulers. If you try to calibrate rulers in the accelerating system using radar measurements made with naturally dilated clocks (i.e proper time) then then "proper radar distances" would not be in agreement with the natural ruler lengths and they would also disagree about the length of a given ruler depending upon which end of the ruler the proper radar distance was measured from. Natural radar measurements would also not agree that when two rulers of equal proper length (L) when laid along side each other would measure 2L when placed end to end. For these reasons natural radar distances are not very good for constructing a sensible coordinate system.
Austin0 said:
This is the differential contraction I was "intuitively" referring to.
yuiop said:
With the clarifications I have made above, I would indeed agree that there is a notion of differential length contraction of an Born accelerating rocket, when observed from a CMIRF.
Passionflower has kindly provided some equations for us to play with and maybe you could try them out and see if things make more sense now?
I have been following with great interest the calculations the two of you have been making but haven't had time to comment.
I have some questions regarding what you and PassionFlower are doing and some areas where I may not correctly understand Born rigidity and Rindler coordinates so I am hoping we can continue this to a point of understanding.
So I would appreciate some clatification on the previous points.
Originally Posted by yuiop
As far as I can tell, the line of simultaneity pivoting about the origin is only true, if the clocks of the accelerating rocket nearer the origin are artificially sped up relative to the clocks nearer the nose.
Originally Posted by DrGreg
True.
austin0...A) I thought the difference in periodicity between the clocks at the front and the back was a result of the difference in proper acceleration and not an artificial contrivance ??
B) That the convergence of L's of S at the pivot event was due to the clocks at the back being naturally dilated relative to the front , not sped up either natrually or artificially . Is this incorrect?
yuiop...If the clocks are left to do their own thing so that they agree with local natural processes, the natural line of simultaneity would be tilted in the opposite direction and would not pass through the origin, no?
Originally Posted by DrGreg
Yes, although now "simultaneity" would bear no relationship to Einstein synchronisation.
Here are some other points I am unsure of:
1) Born rigidity and Dindler coordinates are both based on a natural dilation differential between the front and the back. yes??
This is taken to be equivalent to both a comparable gravitational dilation and a dilation equivalent to a difference in relative velocities??
2) This is assumed to be constant through time with a constant differential factor?
3) A constant acceleration differential would seem to imply a linear increase in relative velocity between the various locations, eg. the front and the back Yes??
4) How does a linear increase in relative velocities work out to be consistent with a constant dilation factor??
5) The coordinate difference in acceleration and resulting relative velocities , as measured in the inertial frame where the accelerated system was initially at rest, must be consistent with the measured Lorentz contraction relative to that inertial frame, correct??
How then could a linear increase in coordinate relative velocities between the front and the back be consistent with the non-linear increase in contraction??
At the begininng stages of acceleration where the contraction is flat and negligable a linear increase would seem to produce too much contraction. At later stages with greater acheived velocities a linear increase in relative velocities would seem to be insufficient to produce the asymptotic increase in contraction, no?
It would seem that an increasing acceleration differential would be needed to be consistent.
On top of this there is the coordinate acceleration dropoff factor of \gamma
3 so at the ponts of the acceleration course, where it would appear to require greater relative acceleration at the rear, the acceleration there would be decreasing by the cubic factor relative to the front, which would be at a lesser relative instantaneous velocity. Yes?
6) A hyperbolic world line for an accelerated system is a graph of the coordinate acceleration of that system as measured in the frame where it was initially at rest correct??
WHile not explicitly an acceleration profile , can't we extract an approximation from this graph by looking at various coordinate time intervals on the vertical axis and the relative increase in the tangent slopes at those points ?
Looking at a graph with this view, it seems to me that the acceleration dropoff, the increase in coordinate time to reach comparable increases in relative velocity are consistent with a single gamma factor. Fairly flat up to high velocities 0.8->0.9+ c where it then becomes increasingly radical.
It does not appear to be consistent with a falloff of \gamma
3 where the increase in coordinate time would become radical at much lower velocities.
Now am I way off here ?? DO you see what I am referring to??
7) You have mentioned that with your calculations for clock calibration you have derived an artificial system that is equivalent to a Rindler system.
COuld you expand upon this as it seems to me that you have achieved a completely different system so I may be completely misinformed regarding Rindler coordinates.
In any case this whole question is fascinating and I hope it progresses. I also apologise for slow responces. Thanks