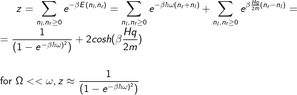Einstein solid state model exercise

In summary, the Einstein solid state model exercise is a theoretical exercise developed by Albert Einstein to model the behavior of solids at low temperatures. It is important for understanding the behavior of solids in materials science and technology, and works by calculating the average energy of oscillators representing atoms in a solid. However, there are limitations to this exercise, such as assuming all atoms are identical. Its real-world applications include studying thermal properties and phase transitions in solids.
  • #1
besebenomo
11
1
Homework Statement
The system is composed of a set of N non-interacting harmonic oscillators which can be described as a two-dimensional Einstein solid model in the x, y plane. Suppose that each oscillator has mass m and charge q and that there is a magnetic field HH directed along the z direction.
Relevant Equations
Compute (when the system at thermal equilibrium at temperature T):
Internal Energy
Magnetization
Specific heat capacity\bigm
ass_1.png


I tried to solve it considering the canonical ensemble (since the system is at the equilibrium with temperature T) and started finding the partition function:
CodeCogsEqn(3).png
The problem is I am not sure if I have done it correctly and need help because I don't really know where to check.
 

Attachments

  • CodeCogsEqn(2).png
    CodeCogsEqn(2).png
    3.1 KB · Views: 108
Last edited:
Physics news on Phys.org
  • #2
Why are you adding the two terms in your expression for the partition sum? You just have to use the expression and do the two sums over ##n_r## and ##n_l##. Obviously these two sums factorize!
 

FAQ: Einstein solid state model exercise

What is an Einstein solid state model exercise?

The Einstein solid state model exercise is a theoretical exercise used to explain the behavior of atoms in a solid state, based on the principles of quantum mechanics and statistical mechanics. It was developed by Albert Einstein in 1907.

How does the Einstein solid state model work?

The Einstein solid state model describes a solid as a collection of atoms that vibrate around their equilibrium positions. These vibrations are quantized, meaning they can only occur at certain energy levels. The model uses statistical mechanics to calculate the average energy of the solid and predict its properties.

What is the significance of the Einstein solid state model?

The Einstein solid state model is significant because it was one of the first attempts to explain the behavior of solids using the principles of quantum mechanics. It also laid the foundation for further developments in the study of solid state physics and materials science.

How is the Einstein solid state model exercise used in research?

The Einstein solid state model exercise is used in research to study the properties of solids, such as thermal conductivity and specific heat capacity. It is also used to understand the behavior of materials at low temperatures, where quantum effects become more prominent.

Are there any limitations to the Einstein solid state model exercise?

Yes, there are limitations to the Einstein solid state model exercise. It assumes that all atoms in a solid are identical and that they interact with each other only through their nearest neighbors. It also does not take into account the effects of external forces, such as pressure and electric fields, on the behavior of the solid.

Similar threads

Help with neutron scattering in solid state physics
Replies
11
Views
2K
Ibach Luth - Solid State 1.11 (QM model for Van der Waals' equation )
Replies
1
Views
1K
Exploring the Grand Partition Function for an Einstein Solid
Replies
2
Views
2K
Solid State Should I buy Kittel's Introduction to Solid State Physics?
Replies
8
Views
2K
Phonon density of states and density of states of free electrons
Replies
3
Views
2K
Solid State Physics: Draw the Dispersion Relation from the Fermi Surface
Replies
1
Views
2K
Assignment on the tight binding model
Replies
1
Views
2K
Solid State Minimal background books for Condensed Matter Theory
Replies
7
Views
400
Why is solid density used in this thermodynamics problem?
Replies
5
Views
1K
Requesting Resources and Animations to understand Solid State Physics
Replies
4
Views
1K

Hot Threads

Recent Insights

Back
Top