larny said:
In space, we know that z = ax + by + c is the eq of a plane.
Now, Einstein's eq for Tau can be written as Tau = gt + hx' where g & h are functions of c & v.
Let's see if it is ...
Tau = gamma*(t-vx/c2)
Tau = gamma*t-gamma*vx/c2
Given c is invariant and v a variable "held constant" (since motion inertial), then ...
Tau = gamma*t-gamma*vx/c2 ... call gamma "g", then ...
Tau = g*t-g*vx/c2
Tau = gt-(gv/c2)x ... call gv/c2 a constant "h" ...
Tau = gt-hx
Now if in terms of x', where x = x'+vt ...
Tau = gt-hx
Tau = gt-h(x'+vt)
Tau = gt-hx'-hvt
Tau = (gt-hvt)-hx'
Tau = (g-hv)t-hx' ... call g-hv a constant "G" ...
Tau = Gt-hx'
So, I say you are right. That said, wrt your question regarding whether Tau is a plane ...
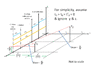
First, a plane is 2 dimensional in 3-space. Let's assume that a plane in 4-space (4d spacetime) is by anaolgy "a volume". I see Tau as a point in time, which may be considered a volume of 3-space (X,Y,Z) at that time Tau. X would be a point in space, which may be considered a volume of 3-space (Y,Z,Tau) at that location X. Y would be a point in space, which may be considered a volume of 3-space (X,Z,Tau) at that location Y. Z would be a point in space, which may be considered a volume of 3-space (X,Y,Tau) at that location Z. The intersection of all four of these 3d-volumes (the LT resolved values) should be a single point in 4-space (ie 4d spacetime ... X,Y,Z,Tau).
larny said:
Then, when we "substitute x' for its value" Tau can be written as Tau = pt + q where p & qx are functions of c & v.
Indeed.
Tau = Gt-hx' ... given x' is a variable "held constant", then call -hx a constant q ...
Tau = Gt+q
larny said:
So my question is - if the eq for z is a plane in space, then I asume that the eqs for Tau are also planes?
Einstein seems to imply this by his comment "it is clear that the equations must be linear on account of the properties of homogeneity which we attribute to space and time"
I know we are talking about space time, but an equation is an equation, so I don't understand why the Tau "vectors" are not perpendicular to the x - t plane.
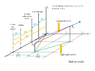
You know, this is an interesting question actually. We assume that time t is perpendicular to x, and time Tau perpendicular to X. This much is certain. Are they? Mathematically, we set them orthogonal to each other because they are independent variables. However, should Tau be perpendicular to x or t? Should t be perpendicular to X or Tau? Well if they should, then Tau and t must be perpendicular to each other. Einstein's LT's define how points in one system are transformed into the other system, both inertial. Therefore, the 2 systems are not independent "of each other", but rather related per the LTs. The LTs are these ...
Tau = gamma*(t-vx/c
2)
X = gamma*(x-vt)
Y = y
Z = z
where gamma = 1/(1-v
2/c
2)
1/2
So Y and y should be parallel, and Z and z should be parallel. Tau & t should not be parallel, and X & x should not be parallel. They should not be orthogonal either, because they are "always" dependent upon each other, being transformations between 2 differing systems of relative v>0. There exists an angle between the Tau and t axes and X and x axes, which depends only on the relative v.
BTW ... I don't see a problem with modeling Tau perpendicular to the x,t plane, so long as your Tau values properly relate to the other system (x and t) per the LTs. It's not the typical way of presenting a spacetime illustration though. Modeling it as such comes at an expense wrt overall meaning of the mechanism, IMO.
GrayGhost