Discussion Overview
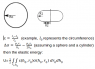
The discussion revolves around calculating the elastic energy stored in a balloon filled with glass beads when it is squeezed, transforming from a spherical shape to a more flattened form. Participants explore the complexities of this problem, including material properties, deformation behavior, and the implications of different assumptions.
Discussion Character
- Exploratory
- Technical explanation
- Debate/contested
- Mathematical reasoning
Main Points Raised
- One participant asks for help in calculating the elastic energy stored in a balloon when squeezed into a different shape.
- Another participant questions whether the elasticity of the balloon material affects the energy calculation, suggesting that it likely does.
- Some participants argue that the problem is ill-defined and may not yield a meaningful answer without clearer parameters.
- Concerns are raised about the complexity of the problem, including the need for a detailed kinematic and material stress analysis.
- Participants discuss the importance of the packing response of the glass beads and the deformational behavior of the rubber in the analysis.
- Suggestions are made to start with simpler assumptions, such as modeling the balloon as containing air instead of glass beads.
- There are recommendations to develop strain energy equations and stress equilibrium equations for the rubber cover, considering the three-dimensional nature of the deformations.
Areas of Agreement / Disagreement
Participants express differing views on the feasibility and practicality of the problem, with some suggesting it may not be worth pursuing due to its complexity. There is no consensus on the best approach to take or the assumptions that should be made.
Contextual Notes
The discussion highlights the limitations of the problem's definition and the assumptions that may need to be made regarding material properties and deformation behavior. The complexity of the interactions between the balloon material and the contents is acknowledged.
Who May Find This Useful
This discussion may be of interest to those studying material science, mechanical engineering, or anyone involved in research related to elastic materials and their behavior under stress.