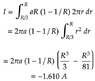SUMMARY
The discussion centers on the correct formulation of current density in cylindrical conductors, specifically addressing the equations $$J(r)=\alpha r (1-\frac{r}{R})$$ and $$J(r)=ar(1-\frac{1}{R})$$. Participants highlight that both formulas are dimensionally incorrect, as the units of the constant $$\alpha$$ are A/m². The consensus suggests that the correct expression for current density should be $$J(r)=a(1-\frac{r}{R})$$ to ensure it decreases linearly from the axis to the surface of the conductor.
PREREQUISITES
- Understanding of current density and its significance in electrical engineering.
- Familiarity with cylindrical coordinate systems in physics.
- Knowledge of dimensional analysis in equations.
- Basic principles of electric current and resistance.
NEXT STEPS
- Study the derivation of current density equations in cylindrical conductors.
- Learn about dimensional analysis and its application in physics equations.
- Explore the implications of current density variations on electrical conductivity.
- Review the principles of electric fields and their relationship with current density.
USEFUL FOR
Electrical engineers, physics students, and anyone involved in the study of electromagnetism and current flow in conductors will benefit from this discussion.