Electric Field acting on a point charge

[guyvsdcsniper]

Homework Statement

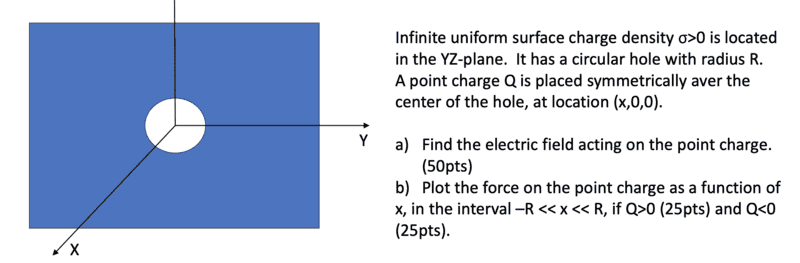
Infinite uniform surface charge density σ>0 is located
in the YZ-plane. It has a circular hole with radius R.
A point charge Q is placed symmetrically aver the
center of the hole, at location (x,0,0).

Relevant Equations

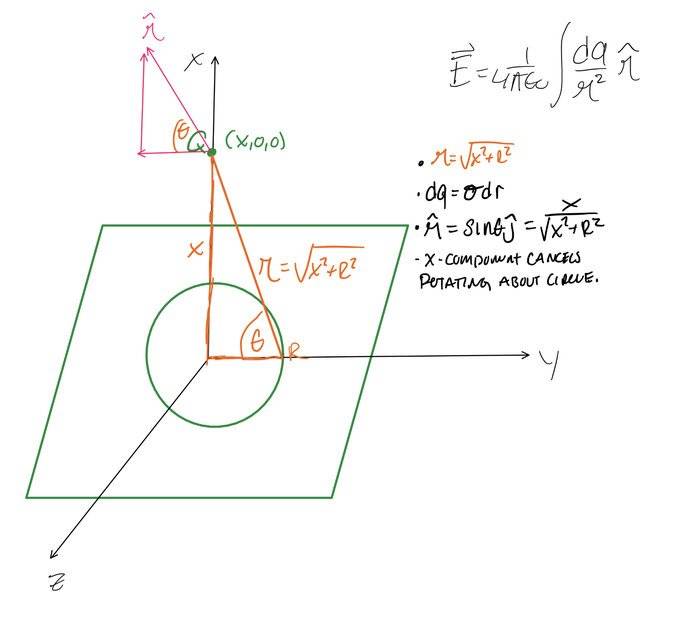
E=dq/r^2

I believe I have all parameters set up correctly to evaluate part A of this problem but I am unsure of the bounds.

I can't integrate from 0 to R because that part of this sheet has a hole there. I need to integrate from R to the other end of the sheet.

Im not sure how I would figure out the upper limit, the end of the sheet.

I thought about evaluating this as a ring first where dq= λdx , and setting the limits from 0 -2pi*r. Then I can use the electric field of that ring and convert λ = σdr. But then I would still need to integrate from R to the end of the sheet, which I don't what that is. Even if I did do that, that would give field of a disk, it doesn't account for the pointed corners of the sheet.

 

[Blanchdog]

The Y-Z plane is infinite in all directions and so has no shape to speak of besides being flat. As such, your limit is infinity regardless of the direction you integrate in.

 

[guyvsdcsniper]

The Y-Z plane is infinite in all directions and so has no shape to speak of besides being flat. As such, your limit is infinity regardless of the direction you integrate in.

That does make sense. Then my approach wouldn't work. How can I approach this?

 

[Delta2]

I am not sure in what I 'll be saying but I think an alternative approach to this is to:

1. Calculate the E-field $\vec{E_1}(\vec{r})$ from a hypothetical circular solid disk of radius R. You might have work this in another problem of your book
2. Calculate the field $\vec{E_2}(\vec{r})$ from a hypothetical solid infinite surface (ok this is easy and covered in most textbooks)
3. The E-field from the surface with the hole is equal to $\vec{E}=\vec{E_2}-\vec{E_1}$.

 

[Blanchdog]

That does make sense. Then my approach wouldn't work. How can I approach this?

There are two ways to do it, an easy way and a hard way.

The easy way is to realize that symmetry is a beautiful thing.

The hard way is to calculate the E field of an infinite charged plane and the E field due to a charged disc, then superimpose the two with the disc having a negative charge distribution. Note that while the E field of the infinite plane does not depend on x, the E field due to the disc does. It does appear that in part b you will need the hard way, getting E as a function of x.

 

[guyvsdcsniper]

There are two ways to do it, an easy way and a hard way.

The easy way is to realize that symmetry is a beautiful thing.

The hard way is to calculate the E field of an infinite charged plane and the E field due to a charged disc, then superimpose the two with the disc having a negative charge distribution. Note that while the E field of the infinite plane does not depend on x, the E field due to the disc does. It does appear that in part b you will need the hard way, getting E as a function of x.

I figured it out using the superposition method.

But now I am curious, how can you approach this doing symmetry?

 

[Blanchdog]

I figured it out using the superposition method.

But now I am curious, how can you approach this doing symmetry?

In part a we are evaluating the electric field at a point with perfectly symmetric amounts of charge in each direction. So the E field is just zero.

 

[Delta2]

In part a we are evaluating the electric field at a point with perfectly symmetric amounts of charge in each direction. So the E field is just zero.

This might be correct cause I think the superposition method also gives $E=E_2-E_1=0-0=0$!

 

[Hall]

I don't think I have understood the question properly because if the charge is on the surface (or on the plane of surface) then evidently the force on it will be zero, but I think the question is trying to say that the infinite surface of charge density sigma is in YZ plane and passing through x=0. Then there is a hole of radius R on the surface and we need to find the force on a charged particle which lies at (x,0,0).

 

[Blanchdog]

I don't think I have understood the question properly because if the charge is on the surface (or on the plane of surface) then evidently the force on it will be zero, but I think the question is trying to say that the infinite surface of charge density sigma is in YZ plane and passing through x=0. Then there is a hole of radius R on the surface and we need to find the force on a charged particle which lies at (x,0,0).

At (x, 0, 0), the force $F = qE$ is indeed zero because $E = 0$ at that point. As one varies the value of x away from zero however, the E field (and thus the force) become non-zero.

 

[Hall]

At (x, 0, 0), the force $F = qE$ is indeed zero because $E = 0$ at that point. As one varies the value of x away from zero however, the E field (and thus the force) become non-zero.

The point (x,0,0) doesn't lie on the plane of infinite surface of charge density sigma.

If it lies, then yes the force is zero.

 

[guyvsdcsniper]

I don't think I have understood the question properly because if the charge is on the surface (or on the plane of surface) then evidently the force on it will be zero, but I think the question is trying to say that the infinite surface of charge density sigma is in YZ plane and passing through x=0. Then there is a hole of radius R on the surface and we need to find the force on a charged particle which lies at (x,0,0).

My interpretation was that this does not lie on the plane of y and z, its above at a point x.

I think that makes the most sense.

 

[Blanchdog]

My interpretation was that this does not lie on the plane of y and z, its above at a point x.

I think that makes the most sense.

You're right, you're right, I misread (x, 0, 0) as being a point in the plane, not on the x axis. So to amend my earlier statements, at the point (0, 0, 0) the E field and force are both zero, but as the point charge is moved along the x-axis the E field and force acting on it become non zero.

 

[guyvsdcsniper]

So after doing all the work, I came out with

.

How do i go about ploting this as a function of x? According to my answer, E would be proportional to x, so would it just be a straight line from -R to R? This kinda makes sense since the field of a sheet is sigma/2epsilon

 

[Blanchdog]

So after doing all the work, I came out with

.

That looks right to me, ignoring the typo on the square root. It would not be a straight line however, as you can see by x appearing in the denominator. Instead, look for something that begins to look like the electric field of the infinite plane as x become large.

 

[guyvsdcsniper]

That looks right to me, ignoring the typo on the square root. It would not be a straight line however, as you can see by x appearing in the denominator. Instead, look for something that begins to look like the electric field of the infinite plane as x become large.

Thank you for catching the typo, and I completely missed the x^2 in the denominator.

Im trying to picture what you said but I am completely lost.

 

[guyvsdcsniper]

You are varying x by some arbitrary amount. We know it will be perfectly mirrored on either side of 0, so let's set the lower bound as zero and the upper bound as some arbitrary number X. What happens to the equation as X becomes large, given that there is an x^2 in the denominator and only an x in the numerator?

That means that the denominator would grow faster, approach infinity and make the fraction equal to zero?

 

[Blanchdog]

Thank you for catching the typo, and I completely missed the x^2 in the denominator.

Im trying to picture what you said but I am completely lost.

You are varying x by some amount, but we know that it will be perfectly mirrored on either side of zero so let's set zero as the lower bound for a plot of what's going on. As mentioned before, E(0) = 0 so that's an easy starting point for your graph. Next, what happens as x becomes large compared to R?

 

[Blanchdog]

That means that the denominator would grow faster, approach infinity and make the fraction equal to zero?

Sorry I deleted that because of a mistake, the fraction goes to 1 rather than zero. See post #18.

 

[guyvsdcsniper]

You are varying x by some amount, but we know that it will be perfectly mirrored on either side of zero so let's set zero as the lower bound for a plot of what's going on. As mentioned before, E(0) = 0 so that's an easy starting point for your graph. Next, what happens as x becomes large compared to R?

As x becomes large compared to R, we can ignore R, then we would have √x², which is equal to x, and then x/x would equal 1, so E would be constant?

But that can't be right since you said earlier it won't be a straight line.

 

[Blanchdog]

It isn't, its asymptotic. Essentially as you move further away from the missing disk, the electric field looks more and more just like the field from the charged plane, which is constant.

 

[guyvsdcsniper]

It isn't, its asymptotic. Essentially as you move further away from the missing disk, the electric field looks more and more just like the field from the charged plane, which is constant.

Im an idiot. I should have said asymptotic. That was I was trying to say but for some reason I kept saying straight line.

So it should look like this right?

 

[Blanchdog]

Electric fields are always continuous, so this cannot be correct. However, if you were to bend the ends of those two lines together at the origin that would pretty much be it. Near the disk the point charge is affected by the disk's presence, it's only further away from the disk that the magnitude of the E field becomes constant.

 

[guyvsdcsniper]

Electric fields are always continuous, so this cannot be correct. However, if you were to bend the ends of those two lines together at the origin that would pretty much be it. Near the disk the point charge is affected by the disk's presence, it's only further away from the disk that the magnitude of the E field becomes constant.

That makes sense. Thank you so much for all your help and walking me through the thought process of this whole problem. I greatly appreciate it.