Electric field at a point within a charged circular ring

[vcsharp2003]

Homework Statement

A charged circular non-conducting ring of radius $R$ has a charge density of $\lambda$ C/m. Would the electric field at point P as shown in diagram be zero? Explain the reason for your answer.

Relevant Equations

$E=\dfrac {kq} {r^2}$ where E is electric field magnitude due to a point charge q at a point that is distant r from the charge q

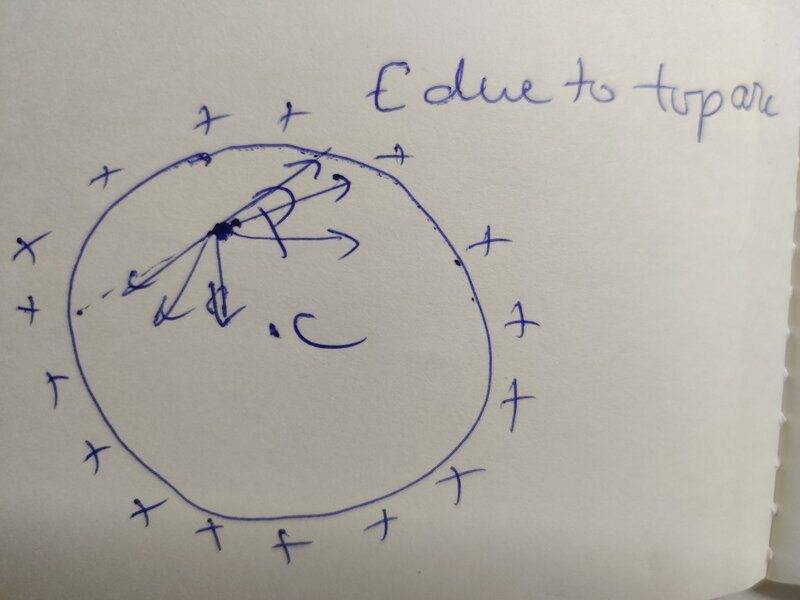
I have broken the ring into a top arc and a bottom arc.

First, let's assume an imaginary charge of +1 C is placed at point P. We will determine the force on this unit charge from top and bottom arcs.

The charges in the top arc will result in electric fields that will all cancel each other perpendicular to line CP leaving us with a net electric field pointing radially inward along the line CP. This is shown in diagram.

Similarly, the charges in bottom arc will result electric field vectors that will cancel each other perpendicular to line CP leaving us with a net electric field pointing radially outward along the line CP. This is shown in diagram.

After above analysis, I am confused since it's difficult to reason whether radial outward electric field at point P will be greater than or less than or equal to the radially inward electric field at the same point.

 

[vcsharp2003]

I came up with another answer which seems like the correct one.

Consider a Gaussian surface that is a sphere centered about the center of circular ring and having a radius of $\dfrac {2R} {3}$.

Due to Gauss's law electric flux through this Gaussian surface is zero since it has no enclosed charge.
$\oint \vec E \cdot \vec {dA} = 0$

But, how can we conclude that E = 0 at every point on the Gaussian surface from above equation of electric flux?

 

[haruspex]

You could try writing down the integral for the net field at P and look for extrema as the distance of P from the centre of the hoop varies.

 

[Delta2]

I came up with another answer which seems like the correct one.

Consider a Gaussian surface that is a sphere centered about the center of circular ring and having a radius of $\dfrac {2R} {3}$.

Due to Gauss's law electric flux through this Gaussian surface is zero since it has no enclosed charge.
$\oint \vec E \cdot \vec {dA} = 0$

But, how can we conclude that E = 0 at every point on the Gaussian surface from above equation of electric flux?

Gauss's law in integral form isn't much useful here because we can't combined it with a useful symmetry argument. There isn't spherical symmetry or cylindrical symmetry, just a circular symmetry if I can call it that way which isn't useful for Gauss's law.

I think for this problem one should write the so called "Coulomb integral" in polar coordinate system. In the plane of the ring there should be only a radial component for the electric field.

As for if the field would be radially inwards or outwards, it will be radially inwards if the ring is positively charged. To see why imagine how the electric field would look like very near the circumference of the ring and from the inside and outside of the ring.

 

[haruspex]

As for if the field would be radially inwards or outwards, it will be radially inwards if the ring is positively charged. To see why imagine how the electric field would look like very near the circumference of the ring and from the inside and outside of the ring.

It's not that simple. You could apply the same reasoning near the inside surface of a uniformly charged sphere, and we know how that turns out.

 

[Delta2]

It's not that simple. You could apply the same reasoning near the inside surface of a uniformly charged sphere, and we know how that turns out.

Yes it is that simple. The sphere is another case, there the field is everywhere zero inside. Here it is zero only at the center.

 

[haruspex]

Yes it is that simple. The sphere is another case, there the field is everywhere zero inside. Here it is zero only at the center.

Yes, we know it is zero inside the sphere, but the argument you propose in post #4 for the ring can also be applied to a sphere: think about the field inside the sphere, close to its surface and you might presume the field from the nearby charges dominates. This proves the argument is unsound.
I don't think there are any shortcuts to avoid dealing with the equations.

 

[Delta2]

Yes, we know it is zero inside the sphere, but the argument you propose in post #4 for the ring can also be applied to a sphere: think about the field inside the sphere, close to its surface and you might presume the field from the nearby charges dominates. This proves the argument is unsound.
I don't think there are any shortcuts to avoid dealing with the equations.

No I don't think the argument is unsound. There must be some reason why it doesn't work in the case of the sphere. There are many differences with the sphere case, there the field at the surface of the sphere is not infinite, but in the ring it becomes infinite.

 

[haruspex]

in the ring it becomes infinite.

... which you know by appealing to the equations, and was not mentioned in your argument in post #4.

 

[Delta2]

... which you know by appealing to the equations, and was not mentioned in your argument in post #4.

Yes well, I know it because I 've done the Coulomb integral in both cases and the difference when integrating is that :

• The differential surface element is $R^2\sin\theta d\theta d\phi$ in the sphere case while the differential linear element in the ring case is $Rd\theta$, R being the radius of the sphere or ring.
• In sphere we assume a finite surface charge density which implies an infinitesimal linear charge density (and infinitesimal charge if we consider a thin ring/circle anywhere in the sphere surface ), while in the ring we have finite linear charge density (and finite charge in the whole ring).

 

[vcsharp2003]

As for if the field would be radially inwards or outwards, it will be radially inwards if the ring is positively charged. To see why imagine how the electric field would look like very near the circumference of the ring and from the inside and outside of the ring.

Also, one could say that the field should be radially inward at P because electric lines of force for a +ve charge must emanate from it rather than end at it. So electric lines of force must be coming out of the +ve charges on ring as we go outwards or inwards from the ring. Does this make sense?

 

[vcsharp2003]

Gauss's law in integral form isn't much useful here because we can't combined it with a useful symmetry argument.

I get it now why Gauss's law cannot be applied. We need to have E such that a constant E can be taken out of the closed surface integral, else Gauss's law is of little use. Thankyou for clearing this symmetry concept in Gauss's law application.

 

[Delta2]

Also, one could say that the field should be radially inward at P because electric lines of force for a +ve charge must emanate from it rather than end at it. So electric lines of force must be coming out of the +ve charges on ring as we go outwards or inwards from the ring. Does this make sense?

Yes this is my basic line of thinking too, coupled with the fact that the direction can not change somewhere in between along the radius from the center to the circumference because that would mean that $\nabla\cdot\mathbf{E}\neq 0$, but we know from Gauss's law in differential form that $\nabla\cdot\mathbf{E}=0$ for all points inside and outside the ring.

 

[vcsharp2003]

Yes well, I know it because I 've done the Coulomb integral in both cases and the difference when integrating is that :

• The differential surface element is $R^2\sin\theta d\theta d\phi$ in the sphere case while the differential linear element in the ring case is $Rd\theta$, R being the radius of the sphere or ring.
• In sphere we assume a finite surface charge density which implies an infinitesimal linear charge density (and infinitesimal charge if we consider a thin ring/circle anywhere in the sphere surface ), while in the ring we have finite linear charge density (and finite charge in the whole ring).

Following the recommendation of applying Coulomb's law at point P, I came up with following analysis.

Consider an infinitesimal element $dl$ as shown in diagram below and determine the field $dE$ due to this element at P. We then integrate from $\theta = 0$ to $\theta = 2 \pi$ to get the net E at point P due to the charges on the ring.

 

[Delta2]

The dE you calculate above is the magnitude of the electric field from the element $Rd\theta$. But you need only its radial component (that is the component along the line CP). You need to multiply it by the cosine of an angle. You can find the sine of that angle by the sine law on the triangle CMP and then use $\cos^2x+\sin^2x=1$ to find the cosine.

P.S $\sin x$ will be a function of $\sin\theta$.

 

[vcsharp2003]

The dE you calculate above is the magnitude of the electric field from the element $Rd\theta$. But you need only its radial component (that is the component along the line CP). You need to multiply it by the cosine of an angle. You can find the sine of that angle by the sine law on the triangle CMP and then use $\cos^2x+\sin^2x=1$ to find the cosine.

Oh, I missed that. I will look at it and rework my solution. Thankyou.

 

[hutchphd]

There isn't spherical symmetry or cylindrical symmetry

There certainly is cylindrical symmetry!
I see nothing in the pure symmetry argument that precludes the field from being exactly zero exactly in the plane of the ring. As pointed out by @haruspex then Gauss or Maxwell must be invoked to show this impossible in the interior. But infinities are not required.

 

[Delta2]

There certainly is cylindrical symmetry!
I see nothing in the pure symmetry argument that precludes the field from being exactly zero exactly in the plane of the ring. As pointed out by @haruspex then Gauss or Maxwell must be invoked to show this impossible in the interior. But infinities are not required.

There is cylindrical symmetry? HOW? I 've done calculations and the field both in magnitude and direction clearly depends on z.
You also say that the field is zero in the plane of the ring, but my calculations don't agree with it.

 

[hutchphd]

Cylindrical symmetry is invariance under rotation about z (not translation along z)

I did not say that E was zero in the plane. I said that symmetry alone does not eliminate that answer.

 

[Delta2]

Cylindrical symmetry is invariance under rotation about z (not translation along z)

I did not say that E was zero in the plane. I said that symmetry alone does not eliminate that answer.

That's not the cylindrical symmetry I know. You seem to have some sort of weak cylindrical symmetry in mind, that is invariance only with respect to the azimuth angle $\phi$. This weak cylindrical symmetry is not much of a use for Gauss's law in integral form.

And yes the symmetry with respect to the azimuth doesn't eliminate the case of E=0 in the interior but neither forces it.

 

[vcsharp2003]

The dE you calculate above is the magnitude of the electric field from the element $Rd\theta$. But you need only its radial component (that is the component along the line CP). You need to multiply it by the cosine of an angle. You can find the sine of that angle by the sine law on the triangle CMP and then use $\cos^2x+\sin^2x=1$ to find the cosine.

P.S $\sin x$ will be a function of $\sin\theta$.

I get the following that results in a complex integral.

 

[hutchphd]

That's not the cylindrical symmetry I know. You seem to have some sort of weak cylindrical symmetry in mind, that is invariance only with respect to the azimuth angle ϕ. This weak cylindrical symmetry is not much of a use for Gauss's law in integral form.

I have no idea what you are talking about. What is the definition you know?

https://en.wikipedia.org/wiki/Circular_symmetry

 

[Delta2]

I have no idea what you are talking about. What is the definition you know?

https://en.wikipedia.org/wiki/Circular_symmetry

This is one of the cases where wikipedia (and you) are wrong. The definition I know requires invariance both in $z$ and $\phi$. Anyway I think you have to agree with me that this cylindrical symmetry you propose is of no use with Gauss's law in integral form.

 

[Delta2]

I get the following that results in a complex integral.View attachment 288020

View attachment 288024

It seems correct to me what you do there except the very last step where you simplify the numerator to $3\cos\theta-2$, what trigonometry identities you used there?

 

[hutchphd]

This is one of the cases where wikipedia (and you) are wrong.

If I am indeed wrong, please supply the appropriate reference explaining your definition, thus allowing me to correct my thinking.
The utility of Gauss's law for an infinite sheet of charge and an infinite charged wire are well known and use a cylindrical surface.

 

[vcsharp2003]

It seems correct to me what you do there except the very last step where you simplify the numerator to $3\cos\theta-2$, what trigonometry identities you used there?

I simplified the expression as below.

 

[Delta2]

If I am indeed wrong, please supply the appropriate reference explaining your definition, thus allowing me to correct my thinking.
The utility of Gauss's law for an infinite sheet of charge and an infinite charged wire are well known and use a cylindrical surface.

Actually I feel that you have to provide me with references where cylindrical symmetry is defined as simply azimuthal symmetry. All the books and notes I 've read, like Griffiths, use cylindrical symmetry as I know it.

The infinite sheet uses another type of symmetry plane symmetry, and the infinite wire uses cylindrical symmetry as I know it with z-invariance.

 

[Delta2]

I simplified the expression as below.

View attachment 288027

Ok I see, then $3\cos\theta-2$ should be inside absolute values inside integral that is $|3\cos\theta-2|$, cause $\sqrt {X^2}=|X|$.

 

[vcsharp2003]

Ok I see, then $3\cos\theta-2$ should be inside absolute values inside integral that is $|3\cos\theta-2|$, cause $\sqrt {X^2}=|X|$.

Is this integral doable without using approximations and numerical analysis?

 

[vcsharp2003]

You could try writing down the integral for the net field at P and look for extrema as the distance of P from the centre of the hoop varies.

Actually, after a lot of thinking the answer is that electric field at P is not zero but pointing radially inwards. Let's consider a case where point P coincides with point C. Then the top arc is a semi-circle and so is the bottom arc. We know from symmetry that all upward components of E at C due to lower semi-circle would cancel with all downward components due to top semi-circle. So electric field at P is zero if P coincides with C.

Now let's move point P upwards from C, then the top arc decreases in its length and the bottom arc increases in its length. This means all downward components of E due to upper arc (smaller than a semi-circle) would be less than the sum of upward components due to lower arc ( bigger than a semi-circle).

Of course, horizontal components would always cancel due to symmetry in all cases of P.

From above argument we can conclude that electric field at P is not zero but pointing radially inward.

 

[Delta2]

Is this integral doable without using approximations and numerical analysis?

Nope I don't think there is an analytical solution, cause wolfram can't find it either.

 

[vcsharp2003]

Nope I don't think there is an analytical solution, cause wolfram can't find it either.

Ok. Then, I guess a qualitative answer is the best answer in this situation.

 

[Delta2]

I think we have done a serious mistake regarding $\cos a$, it becomes negative for a specific range of $\theta$ so it is not always $\sqrt{1-\sin^2a}$ but it becomes $-\sqrt{1-\sin^2a}$ as well. This depends on the position of the point P.

 

[vcsharp2003]

I think we have done a serious mistake regarding $\cos a$, it becomes negative for a specific range of $\theta$ so it is not always $\sqrt{1-\sin^2a}$ but it becomes $-\sqrt{1-\sin^2a}$ as well. This depends on the position of the point P.

That's my mistake.

Yes, for all infinitesimal elements on lower arc, we will have an obtuse angle $\alpha$, while, the same angle will be acute or 90 degrees for elements on top arc.

 

[hutchphd]

All the books and notes I 've read, like Griffiths, use cylindrical symmetry as I know it.

So please explain to me what it is that you "know".
I taught the undergraduate EM course from Griffiths and still have no idea what you are talking about. In particular what is the difference between axial and cylindrical symmetry ? A few sentences should suffice.

 

[vcsharp2003]

Nope I don't think there is an analytical solution, cause wolfram can't find it either.

Did you mean that there is no method available to solve the integral?

 

[Gordianus]

From above argument we can conclude that electric field at P is not zero but pointing radially inward.

Let me consider a point P', radially opposed to P. If I applied the same reasoning, I would conclude the field at P' points radially inward. Therefore, we should have a negative charge (sink) at the center but I can't see that charge.

 

[vcsharp2003]

Let me consider a point P', radially opposed to P. If I applied the same reasoning, I would conclude the field at P' points radially inward. Therefore, we should have a negative charge (sink) at the center but I can't see that charge.

I am not sure if your reasoning is correct. If it's correct, then a positive charge has electric lines of force emanating from it which must be directed towards a negative charge. We know this is not true. A positive charge can exist by itself and have its own electric field independent of a negative charge being paired with it.

 

[hutchphd]

At the center the goes squirting out symmetrically along the +/- z axis. ( The z axis being the axis of symmetry.) So this is OK. Look it up

 

[Gordianus]

I am not sure if your reasoning is correct. If it's correct, then a positive charge has electric lines of force emanating from it which must be directed towards a negative charge. We know this is not true. A positive charge can exist by itself and have its own electric field independent of a negative charge being paired with it.

By convention, field lines start at positive charges and end at negative charges. If I understood your reasoning correctly, at any point inside the ring (except the center) the field points radially inward. Thus, we should have a negative charge at the center.

 

[vcsharp2003]

By convention, field lines start at positive charges and end at negative charges

How about electric field due to an isolated positive charge?

 

[Gordianus]

How about electric field due to an isolated positive charge?

I'd say there are no isolated positive charges. Negative charges must be somewhere, perhaps very far away.

 

[haruspex]

This is one of the cases where wikipedia (and you) are wrong. The definition I know requires invariance both in $z$ and $\phi$. Anyway I think you have to agree with me that this cylindrical symmetry you propose is of no use with Gauss's law in integral form.

Do you have a reference for that?
Apart from one related to GR, all the items I could find online regard cylindrical, circular, azimuthal and axial symmetry as interchangeable terms.
I agree it would be more natural to define cylindrical as also implying translational symmetry along the axis, but the GR item was the only one which seemed to imply that.

 

[vcsharp2003]

I'd say there are no isolated positive charges. Negative charges must be somewhere, perhaps very far away.

Then, there should no electric field at point P. Is that what you're hinting at? Even if electric field is radially outward it would not make any sense since electric lines of force cannot end on postive charge.

My view on this is that there is a 3 dimensional electric field existing due to the ring and the lines of force from the ring will spread in a 3 dimensional manner. Lines of force go inwards from the ring towards C and then curve out towards the axis of the ring as the line approaches the point C. I am not good at depicting it through a diagram, but something like below is how the lines of force would be in 3 dimensional situation about the axis of the ring. The field in the space around the ring is going to be complex, but below diagram looks at the part of the lines of force that appear to be converging at C. They will bend outward towards the ring's axis. Sort of like a funnel pattern on each side of the ring.

 

[Steve4Physics]

Here's a decent video (though a bit long at 13mins) deriving the field at a point inside a charged ring...

 

[hutchphd]

My view on this is that there is a 3 dimensional electric field existing due to the ring and the lines of force from the ring will spread in a 3 dimensional manner.

They will bend outward towards the ring's axis. Sort of like a funnel pattern on each side of the ring.

Yes this is correct for both +z and -z (it is also symmetric up-down). The lines eventually diverge from the z axis and far away it all looks like that of a point charge. I have never seen a pleasant analytic treatment for the near field.

 

[Delta2]

So please explain to me what it is that you "know".
I taught the undergraduate EM course from Griffiths and still have no idea what you are talking about. In particular what is the difference between axial and cylindrical symmetry ? A few sentences should suffice.

Check post #23.
Can you give me an example in Griffiths where this axial/cylindrical symmetry is used together with Gauss's law, cause the two examples you gave just won't do for reasons I explained in previous post of mine.

 

[Gordianus]

I must recognize muy previous posts had a flawed reasoning. The video proved me wrong and intuition can fail.

 

[hutchphd]

Post #23 still says objectively nothing. If you cannot even explain your objection, I shall value your opinion appropriately.

 

[Delta2]

Post #23 still says objectively nothing. If you cannot even explain your objection, I shall value your opinion appropriately.

Post #23 says that the cylindrical symmetry I know has invariance with $z$ as well with $\phi$. You know it only with invariance to $\phi$. If that's objectively nothing and doesn't explain my objection then ok, I would say that your eyes can't see what you don't want to read.