Electric Field at Center of Spherical Half-Shell

[maherelharake]

Homework Statement

The differential area on the surface of a sphere in spherical coordinates is given on inside front cover of textbook, dS=dr sin(θ)dθ dφ. See sect. 1.4.1.

a. Verify that the surface area of a sphere of radius R is 4PiR^2.

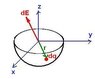
b. Calculate the electric field (all components) at the center of a half-shell of
radius R. The surface of the half-shell is below the xy plane. It has uniform surface charge density, σ. The center of the sphere is also the origin of the coordinate system.

Homework Equations

The Attempt at a Solution

Part A:
I believe the given was supposed to be dS=r^2 sin(θ)dθ dφ. I did this part, assuming the problem was incorrect.
I integrated this as a double integral and got the correct result of 4PiR^2.

Part B:
This is where I need help. I drew the diagram, and am having trouble getting it started. I know the general idea is to take a small section, and find E there, and integrate over the rest of the surface. I am having trouble carrying that idea out though. Any help is appreciated. Thanks in advance.

 

[ehild]

Draw a picture something like the attached one. You need to get the electric field at the centre of the sphere. For a surface element dA at a given position (θ,φ) write dE, the contribution of the charge on dA to the vector of the electric field at the centre. Write all components of dE in terms of the angles θ and φ. Integrate for the half sphere.

ehild

 

[maherelharake]

I think I see what you are saying. Am I on the right track?

 

[maherelharake]

I have tried to think of this in different ways, but made no progress. Any comments for me? Thanks in advance.

 

[noface]

Steve D. got you down?

 

[maherelharake]

Ha not too bad. I'm getting there. Are you in the class?

 

[ehild]

I think I see what you are saying. Am I on the right track?

Not quite... The electric field is a vector, and dE, the contribution of a surface element dA is antiparallel to the radius vector. You can see that the horizontal component of E cancels because of symmetry, but you get the same if you integrate the x ad y components of dE.
The resultant field has only z component. Write down the z component of dE and integrate from 0 to 2pi with respect to φ and from pi/2 to pi with respect to Θ.

ehild

 

[maherelharake]

Ok I think I am very close. I am getting, what I hope is, the correct answer. However, I am off by a factor of -1 at the end. Did I mess up on the first step where I substituted for
-z_prime? I put Rcos(theta), but is it supposed to be -Rcos(theta). Thanks again.

 

[gabbagabbahey]

Did I mess up on the first step where I substituted for
-z_prime? I put Rcos(theta), but is it supposed to be -Rcos(theta). Thanks again.

Yup, that's your error.

 

[maherelharake]

Ok so I should add a negative sign in front of my z_prime, x_prime, and y_prime terms on all three equations. For the bottom two, it won't change it from 0, and for the top one, it will make it correct? I think I got it. Right?

 

[noface]

I am, and I also got the same answer as you. This was the first page that came up when I tried to verify my answer online, and I recognized the problem immediately as Dr. D's.

 

[maherelharake]

Oh ok cool. The people on this forum are really helpful. I recommend it a lot. I think someone else on here is from our class too, because I recognized one of the problems (I didn't look at it closely though).