Electric field created by two charged circular arcs?

[zenterix]

Homework Statement

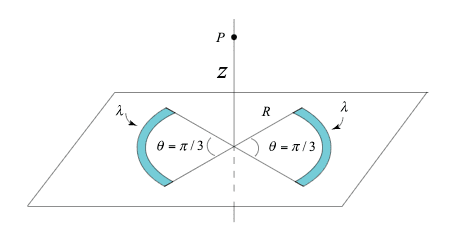
Two circular arcs of radius $R$ are uniformly charged with a positive charge per unit length $\lambda$. The arcs lie on a plane as shown in the figure below. Each arc subtends an angle $\theta=\frac{\pi}{3}$.

What is the direction and magnitude of the electric field anywhere along the $z$ axis that passes through the center of the circular arcs, perpendicular to the plane of the figure?

Relevant Equations

Infinitesimal electric field created by an infinitesimal charge $dq$ on the right-side arc
$$d\vec{E}_{p_r}=\frac{k_e dq}{r_{dq,p}^2}\hat{r}_{dq,p}$$

The strategy will be to figure out what $dq$, $\hat{r}_{dq,p}$, and $r_{dq,p}$ are, plug them into the expression for $d\vec{E}_{p_r}$, then integrate over $d\vec{E}_{p_r}$ to obtain $\vec{E}_{p_r}$, the electric field at $P$ due to the arc on the right.

Then I will repeat the process to calculate $d\vec{E}_{p_l}$ and $\vec{E}_{p_l}$, for the arc on the left. The latter will be basically the same result as for $d\vec{E}_{p_r}$ but with one sign changed.

$$dq=\lambda ds = \lambda R d\theta$$

Here are the original sketch of the problem and my own sketch

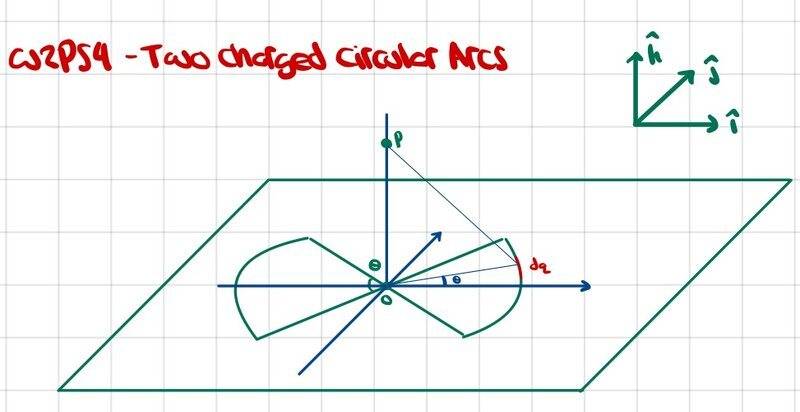
$$\vec{r}_{dq,p}=\vec{r}_{0,p}-\vec{r}_{0,dq}$$

$$\vec{r}_{0,p}=z\hat{k}$$

$$\hat{r}_{0,dq}=\cos{\theta}\hat{i} +\sin{\theta}\hat{j}$$

$$\vec{r}_{0,dq}=R\hat{r}_{0,dq}=R(\cos{\theta}\hat{i} +\sin{\theta}\hat{j})$$

$$\implies \vec{r}_{dq,p}=z\hat{k}-R\cos{\theta}\hat{i} -R\sin{\theta}\hat{j}$$

$$d\vec{E}_{p_r}=\frac{k_e \lambda R d\theta}{(z^2+R^2)^{3/2}}(z\hat{k}-R\cos{\theta}\hat{i} -R\sin{\theta}\hat{j})$$

The expression for $d\vec{E}_{p_l}$ is derived analogously, and the only thing that changes is s sign on $\hat{r}_{0,dq}$

$$\hat{r}_{0,dq}=-\cos{\theta}\hat{i} +\sin{\theta}\hat{j}$$

$$d\vec{E}_{p_l}=\frac{k_e \lambda R d\theta}{(z^2+R^2)^{3/2}}(z\hat{k}+R\cos{\theta}\hat{i} -R\sin{\theta}\hat{j})$$

Now we integrate over $\theta$

$$\vec{E}_{p_r}=\int_{-\frac{\pi}{3}}^{\frac{\pi}{3}} \frac{k_e \lambda R d\theta}{(z^2+R^2)^{3/2}}(z\hat{k}-R\cos{\theta}\hat{i} -R\sin{\theta}\hat{j})$$

$$\vec{E}_{p_l}=\int_{-\frac{\pi}{3}}^{\frac{\pi}{3}} \frac{k_e \lambda R d\theta}{(z^2+R^2)^{3/2}}(z\hat{k}+R\cos{\theta}\hat{i} -R\sin{\theta}\hat{j})$$

We end up with

$$\vec{E}_{p_r}=\frac{k_e \lambda R d\theta}{(z^2+R^2)^{3/2}}(\frac{2\pi z}{3}\hat{z} -R\sqrt{3}\hat{i})$$$$\vec{E}_{p_l}=\frac{k_e \lambda R d\theta}{(z^2+R^2)^{3/2}}(\frac{2\pi z}{3}\hat{z} +R\sqrt{3}\hat{i})$$

Therefore

$$\vec{E}_p=\vec{E}_{p_r}+\vec{E}_{p_l}=\frac{k_e \lambda R d\theta}{(z^2+R^2)^{3/2}}\frac{4\pi z}{3}\hat{k}$$
$$=\frac{\lambda R z}{3\epsilon_0 (z^2+R^2)^{3/2}}\hat{k}$$

I'd like to know if this solution is correct because I am following along on MIT Open Learning Library and this is a practice problem. I am allowed to submit answers, and am given a correct/incorrect feedback. For the expression above, I am getting incorrect, though I can't figure out why.

 

[Steve4Physics]

Hi @zenterix. Your integration limits should be $-\frac {\pi}{6}$ to $+\frac {\pi}{6}$ (to cover a total angle of $\frac {\pi}{3}$ for each arc).

Are you required to do the formal vector/integration method as an exercise? The problem can be solved in a few lines of basic algebra using some simple observations:
- by symmetry, the x and y components of the field at P are zero;
- the magnitude of the field at P from each charge-element (dq) is $dE = \frac {kdq}{z^2 + R^2}$;
- the z-component of $\vec {dE}$ is $dE cos(\phi)$ where $\phi$ is the angle between the z-axis and the line from P to the charge-element.

It's a useful exercise to try as you will see how much easier/quicker the use of symmetry can make a problem.

 

[zenterix]

I can't believe I missed the integral limits! My god.

I am aware of the symmetry of the problem. At this stage I am doing the full calculations to get practice doing the calculus. But I will try to just use symmetry to also get practice with identifying such shortcuts from now on as well.