vcsharp2003
- 913
- 179
- Homework Statement
- The book derives a formula for a point close to the charged conductor and goes on to say that this formula applies to any charged conductor without sharp points. This derived formula is ##E = \frac {\sigma} {\epsilon_o}## where ##\sigma## is the uniform charge density on the surface of conductor. Why is book assuming the formula is only for near points?
- Relevant Equations
- ##E = \frac {\sigma} {\epsilon_o}##
As shown in figure below, the electric field E will be normal to the cylinder's cross sectional A
even for distant points since the charge is distributed evenly all over the charged surface and also the surface is very large resulting in a symmetry. So the derived formula should also apply to distant points.
I am not sure if my reasoning is correct.
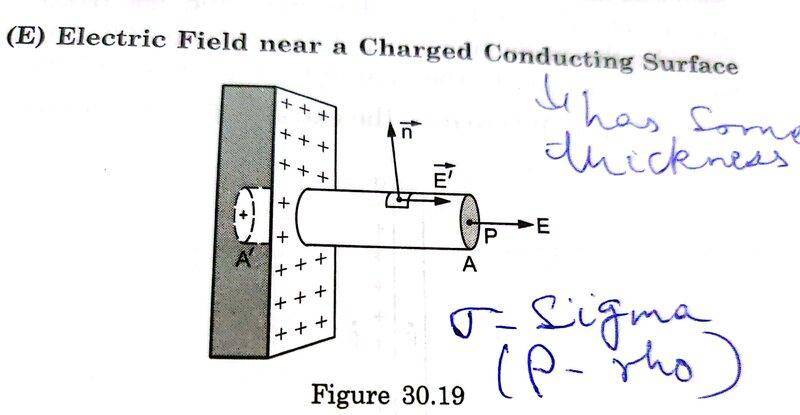
even for distant points since the charge is distributed evenly all over the charged surface and also the surface is very large resulting in a symmetry. So the derived formula should also apply to distant points.
I am not sure if my reasoning is correct.