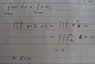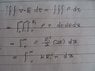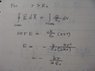Electric field in a cylindrical capacitor

[athrun200]

Homework Statement

A very long question. First let's solve the case for E-field between outer and inner capacitor.

Homework Equations

The Attempt at a Solution

Since there is no charge between the 2 capacitors, the charge density is zero.
By Gauss's law, the integral is zero.

But I know it doesn't make sense, so what's wrong?

 

[I like Serena]

Hi athrun200!

You cannot draw the conclusion that E is zero from this.

What you do have is that the surface integral of E is zero according to Gauss's law.
That means that the flux in of the electric field on one side must equal the flux out of the electric field on the other side.

 

[athrun200]

Hi athrun200!

You cannot draw the conclusion that E is zero from this.

What you do have is that the surface integral of E is zero according to Gauss's law.
That means that the flux in of the electric field on one side must equal the flux out of the electric field on the other side.

After knowing that there is no net flux flow, how can I get E-field?

 

[Dick]

After knowing that there is no net flux flow, how can I get E-field?

Are you sure you know what Gauss' law states? It says the flux through the surface is proportional to the enclosed charge, yes? Between the two cylinders there is definitely a nonzero enclosed charge and a nonzero flux. The outer charge is not 'enclosed' if the radius of the surface is between the radii of the two cylinders. You need to choose a cylindrical surface and use the symmetry of the problem to compute the flux.

 

[athrun200]

Do you mean this?

But I encounter 2 problems.
1. I don't know the range for z.
2. Even I don't the range for z, how can I obtain the E from left hand side?

 

[Dick]

Do you mean this?

But I encounter 2 problems.
1. I don't know the range for z.
2. Even I don't the range for z, how can I obtain the E from left hand side?

That is not Gauss' law. Gauss' law relates a surface integral of the E field to a volume integral of the charge rho. Why do you have a volume integral of div(E)? You don't even need to write component integrals to do this problem. E is equal and pointed outward from your surface everywhere using symmetry, right? So the surface integral is just the multiple of the area of the surface per unit length times E. Ditto on the enclosed charge, it's just the amount of charge enclosed per unit length. Notice you are given the charge in terms of coulombs/meter, i.e. charge per unit length. Just equate them. The z range doesn't matter since everything is 'per unit length'.

 

[I like Serena]

Take anything for the range of z. Let's call it delta z.

On your first scan you wrote a surface integral over a closed surface.
Do you know what it means and what it is for?

Suppose we know what E is, what would be its flux over the surface of the volume that you just integrated?

 

[athrun200]

I thought that it could be easier after applying divergence theorem.

Is it ok now?

 

[athrun200]

Take anything for the range of z. Let's call it delta z.

On your first scan you wrote a surface integral over a closed surface.
Do you know what it means and what it is for?

Suppose we know what E is, what would be its flux over the surface of the volume that you just integrated?

I know how to calculate surface, volume integrals.
And also I know green's and divergence theorem.

I have done a lot of exercises on them and I can master them very well.

But when it comes to physical application, I don't know why it is confusing. Maybe I am not good at physics.:uhh:

 

[I like Serena]

But when it comes to physical application, I don't know why it is confusing. Maybe I am not good at physics.:uhh:

I guess it takes a bit of effort to wrap the mind around what these mathematical theorems mean and what they are for.
That's what these exercises are for! ;)

Is it ok now?

Much better yes. :)

So you've calculated an E here.
But what E is that exactly?
At which coordinates and in which direction would this be the solution for E?

 

[athrun200]

I guess it takes a bit of effort to wrap the mind around what these mathematical theorems mean and what they are for.
That's what these exercises are for! ;)




Much better yes. :)

So you've calculated an E here.
But what E is that exactly?
At which coordinates and in which direction would this be the solution for E?

Between $^{R}1$ and $^{R}2$?
The direction is normal to the surface?

 

[I like Serena]

Between $^{R}1$ and $^{R}2$?
The direction is normal to the surface?

Close.
A little more accurate would be that you solved the radial component of E, which is indeed normal to the surface.

At which radius did you do the integration?

Btw, this brings up the question what the other components are.
Any thoughts on what the component of E in the z direction is?
And in the theta direction?

 

[athrun200]

Close.
A little more accurate would be that you solved the radial component of E, which is indeed normal to the surface.

At which radius did you do the integration?

Btw, this brings up the question what the other components are.
Any thoughts on what the component of E in the z direction is?
And in the theta direction?

Do you mean that despite that we consider the case for R1 to R2, the solution of E is form 0 to R1?(Since the range of integral is 0 ro R1)

It seems E in the z direction is zero, otherwise current flows inside.

E is constant for all value of theta.

 

[I like Serena]

Do you mean that despite that we consider the case for R1 to R2, the solution of E is form 0 to R1?(Since the range of integral is 0 ro R1)

It seems E in the z direction is zero, otherwise current flows inside.

E is constant for all value of theta.

No, you did a "surface" integral for E, not a volume integral (you did that for the charge).

Basically you selected an cylindrical object with a certain radius and height.
You integrated E over the surface of this cylinder.
And you integrated the charge over the volume of this cylinder.

What was the radius of this cylinder?
Or rather, at what radius did you calculate E?
Suppose we would pick another radius r between R1 and R2, what would the radial component of E be then?
And yes, the z component of E is zero, because otherwise a current would flow in the z direction, which would make no sense since the charge at higher z is the same as the charge at lower z.
Now if E is constant for all value of theta in the direction of theta, what would happen?

 

[athrun200]

No, you did a "surface" integral for E, not a volume integral (you did that for the charge).

Basically you selected an cylindrical object with a certain radius and height.
You integrated E over the surface of this cylinder.
And you integrated the charge over the volume of this cylinder.

What was the radius of this cylinder?
Or rather, at what radius did you calculate E?
Suppose we would pick another radius r between R1 and R2, what would the radial component of E be then?



And yes, the z component of E is zero, because otherwise a current would flow in the z direction, which would make no sense since the charge at higher z is the same as the charge at lower z.



Now if E is constant for all value of theta in the direction of theta, what would happen?

Oh, I know what you are talking about.
The value of E I have obtained is located at R1.
The value of E decrease when we move from R1 to R2.

So E is not constant in the direction of theta, it is decreasing.

 

[I like Serena]

Oh, I know what you are talking about.
The value of E I have obtained is located at R1.
The value of E decrease when we move from R1 to R2.

So E is not constant in the direction of theta, it is decreasing.

Indeed the value of E would decrease when we move from R1 to R2, but by how much?
So E is not constant in the direction of r, it is decreasing.

However, in the direction of theta things are different.
Because that is at constant r.

I get the impression you're mixing up something.
E is a vector field.
That means that at any point (r, θ, z) E has 3 components.
An E_r component in the direction of r.
An E_θ component in the direction of θ.
And an E_z component in the direction of z.

I think we've established that E_z is zero.
And that E_r is decreasing when r increases.
The remaining question is, what is E_θ?

 

[athrun200]

Indeed the value of E would decrease when we move from R1 to R2, but by how much?
So E is not constant in the direction of r, it is decreasing.

However, in the direction of theta things are different.
Because that is at constant r.

I get the impression you're mixing up something.
E is a vector field.
That means that at any point (r, θ, z) E has 3 components.
An E_r component in the direction of r.
An E_θ component in the direction of θ.
And an E_z component in the direction of z.

I think we've established that E_z is zero.
And that E_r is decreasing when r increases.
The remaining question is, what is E_θ?

E_θ= E_r because you have just mentioned that E depends on r.

For the question of how much E_r decrease, I totally have no idea.
Can I obtain it via diff.?

 

[I like Serena]

E_θ= E_r because you have just mentioned that E depends on r.

No, this is not right.
Basically, the only thing I said, is that E_r depends on r.

Actually you have 3 functions here that you need to solve:
E_r(r, θ, z)
E_θ(r, θ, z)
E_z(r, θ, z)

The component E_r(r, θ, z) it the one (the *only* one) that is perpendicular to the surface of the cylinder that you integrated.
This component will be the same for any θ and for any z.
But it will change if r changes.
We typically indicate this dependency by writing E_r = E_r(r).

Can you say something about the dependencies of E_z(r, θ, z)?
Is it dependent of either r, θ, or z?
And E_θ(r, θ, z)?

For the question of how much E_r decrease, I totally have no idea.
Can I obtain it via diff.?

This time round you integrated over a cylinder with radius R1.
Can you do the same integration over a cylinder with radius r?

 

[athrun200]

No, this is not right.
Basically, the only thing I said, is that E_r depends on r.

Actually you have 3 functions here that you need to solve:
E_r(r, θ, z)
E_θ(r, θ, z)
E_z(r, θ, z)

The component E_r(r, θ, z) it the one (the *only* one) that is perpendicular to the surface of the cylinder that you integrated.
This component will be the same for any θ and for any z.
But it will change if r changes.
We typically indicate this dependency by writing E_r = E_r(r).

Can you say something about the dependencies of E_z(r, θ, z)?
Is it dependent of either r, θ, or z?
And E_θ(r, θ, z)?

This time round you integrated over a cylinder with radius R1.
Can you do the same integration over a cylinder with radius r?

It seems E_z and E_θ are independent of the three variables.
The value of them are 0 too.
If it is the case, I have only 1 equation that is E_r.

I am still very puzzle on this question. Can you do the case of R₁<r<R₂ for me?

I would like to have an example as a reference and try to do the rest of the cases.
Thx!

 

[I like Serena]

It seems E_z and E_θ are independent of the three variables.
The value of them are 0 too.
If it is the case, I have only 1 equation that is E_r.

I am still very puzzle on this question. Can you do the case of R₁<r<R₂ for me?

I would like to have an example as a reference and try to do the rest of the cases.
Thx!

Exactly.
E_z = E_θ = 0

As doing the case for you - it's exactly what you did, except with r instead of R1 on the left hand side where you have the surface integral of E.
This means you integrate over a cylinder that is bigger than the inner cylinder.
The contained charge is the same (the right hand side), but the surface integral changes.

 

[athrun200]

Is it the answer?

For this case, I know the value of E is zero since no current flows. But how to obtain the answer mathematically?

In this case, I am not sure for 2 things.
1. dose the inner surface afect the integral?
2. what is the value of Q? -k only or -k+k?

 

[IDOGAWACONAN]

The remaining question is, what is E_θ?

Hi
Eθ is also 0
Beside Gauss's law there is also a circuital theorem says that the integral of E*dl at a closed circuit is 0(just electrostatic field).

 

[athrun200]

Hi
Eθ is also 0
Beside Gauss's law there is also a circuital theorem says that the integral of E*dl at a closed circuit is 0(just electrostatic field).

In fact I have answered that question, and we are now page 2.
Can you help me to check if I get the correct answer?

 

[I like Serena]

Is it the answer?

You have an 'r' on the right hand side of your calculation, which should still be R1.
However in the result you apparently corrected that.

But in the result you have a pi that you forgot to cancel.

For this case, I know the value of E is zero since no current flows. But how to obtain the answer mathematically?

You're integrating over a cylinder here that is entirely within the inner cylinder.
This means there is no enclosed charge, so the volume integral (right hand side of your equation) is zero.
This means the surface integral (on the left hand side) is zero as well, meaning Er is zero as well.

In this case, I am not sure for 2 things.
1. dose the inner surface afect the integral?
2. what is the value of Q? -k only or -k+k?

1. Yes.
2. What is the sum of all enclosed charges?
Because you need the volume integral of the enclosed charges.

 

[athrun200]

You have an 'r' on the right hand side of your calculation, which should still be R1.
However in the result you apparently corrected that.

But in the result you have a pi that you forgot to cancel.





You're integrating over a cylinder here that is entirely within the inner cylinder.
This means there is no enclosed charge, so the volume integral (right hand side of your equation) is zero.
This means the surface integral (on the left hand side) is zero as well, meaning Er is zero as well.





1. Yes.
2. What is the sum of all enclosed charges?
Because you need the volume integral of the enclosed charges.

It seems sum of enclosed charges is zero because k-k=0

 

[I like Serena]

It seems sum of enclosed charges is zero because k-k=0

Yes, it seems that way, and it is. ;)

 

[athrun200]

Yes, it seems that way, and it is. ;)

However, when I think of it, it doesn't make sense.
I think there will be electric field outside the 2 capacitor.

And from the answer of potential, the E electric isn't 0 in this case/.

 

[I like Serena]

Whaaaaat? You peeked! ;)

Ah well, did you try to calculate the gradient of phi outside the capacitor?
What is it?

Actually, I'm a bit surprised the book gives this as a solution.
You are free to select the integration constant in this problem, but usually it is taken such that the potential is zero at infinity.
Here they have chosen to have the potential zero inside the inner cylinder.


Btw, now that I see the solution, I suddenly realize the volume integral you calculated is wrong. Sorry.
You calculated the entire volume and assumed the charge density was constant everywhere and equal to k.
But it isn't. The charge is k per meter just on the outside of the cylinder.

To be clear:
For a cylinder of radius r and height delta z, with r between R1 and R2, the calculation is:
$$\iint\kern-1.4em\bigcirc\kern.7em E \cdot dA = \iiint \frac \rho {\epsilon_0} dV$$
$$E_r(r) \cdot 2 \pi r \Delta z = \frac k {\epsilon_0} \Delta z$$

 

[athrun200]

Whaaaaat? You peeked! ;)

Ah well, did you try to calculate the gradient of phi outside the capacitor?
What is it?

Actually, I'm a bit surprised the book gives this as a solution.
You are free to select the integration constant in this problem, but usually it is taken such that the potential is zero at infinity.
Here they have chosen to have the potential zero inside the inner cylinder.


Btw, now that I see the solution, I suddenly realize the volume integral you calculated is wrong. Sorry.
You calculated the entire volume and assumed the charge density was constant everywhere and equal to k.
But it isn't. The charge is k per meter just on the outside of the cylinder.

To be clear:
For a cylinder of radius r and height delta z, with r between R1 and R2, the calculation is:
$$\iint\kern-1.4em\bigcirc\kern.7em E \cdot dA = \iiint \frac \rho \epsilon_0 dV$$
$$E_r(r) \cdot 2 \pi r \Delta z = \frac k \epsilon_0 \Delta z$$

Oh! I suddenly know why.
The electric field out the outer cylinder is zero.
However it doesn't imply that the potential is zero.
Instead, it means no change of potential.

Since at r=R2, the potential=$\frac{kln(R1/R2)}{2\pi \epsilon_0}$
Thus the potential outside the cylinder is still $\frac{kln(R1/R2)}{2\pi \epsilon_0}$

Am I right?

 

[I like Serena]

Oh! I suddenly know why.
The electric field out the outer cylinder is zero.
However it doesn't imply that the potential is zero.
Instead, it means no change of potential.

Since at r=R2, the potential=$\frac{kln(R1/R2)}{2\pi \epsilon_0}$
Thus the potential outside the cylinder is still $\frac{kln(R1/R2)}{2\pi \epsilon_0}$

Am I right?

Yep.
The potential (outside the outer cylinder) does not depend on any coordinate, so its derivative (the electric field) is zero.

 

[IDOGAWACONAN]

In fact I have answered that question, and we are now page 2.
Can you help me to check if I get the correct answer?

...Sorry I post it on page 1 but it is now on page 2...I don't know why...
It seems all questions are solved :-)

 

[athrun200]

Thanks everyone!