- #1
APUGYael
- 41
- 1
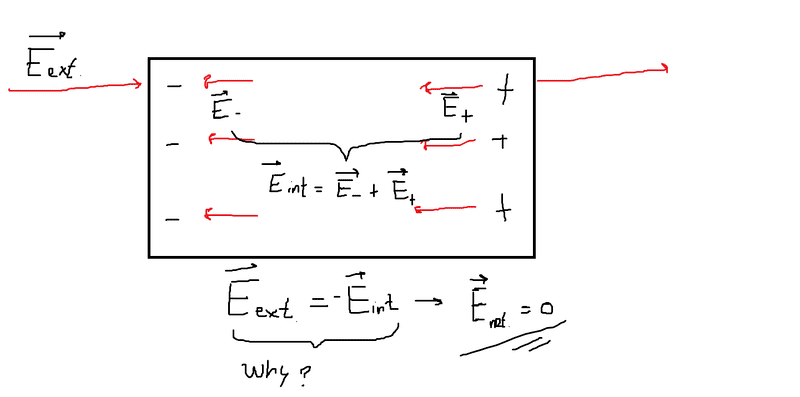
The electric field inside a conductor is zero. Or: the internal electric field is equal in magnitude but opposite in direction to the external electric field, so that the net electric field inside the conductor is zero.
Why is this? The part where I am confused is why the magnitude is equal.
Is it just that we measured the electric field inside to be zero, and so concluded that the internal electric field should oppose the external electric field?
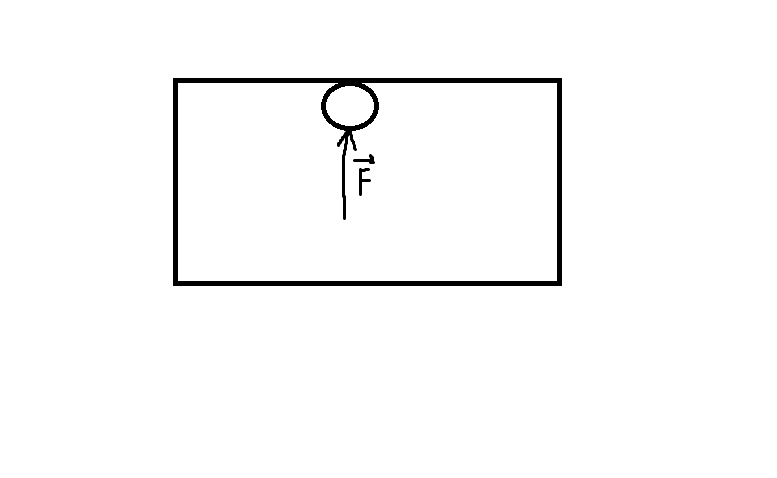
Bonus question: What would happen to a particle (of an object) near the surface if you put a force on it pointing outward of the object. Would it jump out?
Looking forward to a response.
-Y
Why is this? The part where I am confused is why the magnitude is equal.
Is it just that we measured the electric field inside to be zero, and so concluded that the internal electric field should oppose the external electric field?
Bonus question: What would happen to a particle (of an object) near the surface if you put a force on it pointing outward of the object. Would it jump out?
Looking forward to a response.
-Y