Waxterzz
- 82
- 0
Find E(r) inside and outside a uniformly charged spherical volume by superposing the electric fields
produced by a collection of uniformly charged disks.
a+b) Given equations, sketch of problem
This is the equation in the handbook for a disk (but in the exercises the z becomes x, without loss of generality)
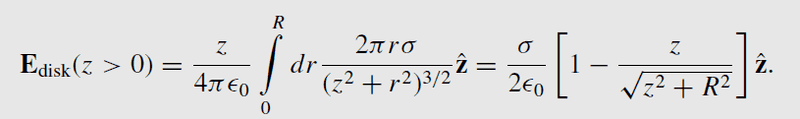
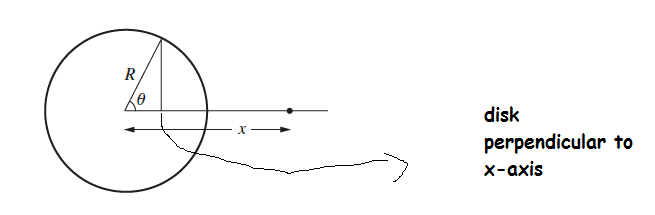
So by varying theta, he wants you to superpose the disks, to form a solid sphere. The disks are x- R* cos(theta) removed.
[/B]

So he changes in the equation for the disk,the nominator z was the distance from the evaluation point to the center of the disk, this was z. This now becomes x-R*cos(theta). The denominator was the distance from the rim of the disk to the evaluation point, this was in the equation just the pythagoras rule, now it varies with theta because you have a superposition of different disks, so the pythagoras rule becomes the cosine rule. I kinda get these alterations.
What I don't get:
But I don't really get how he substitutes the surface charge density with this term with rho in? The term d(surface charge charge) = rho * R * sin (theta) * d(theta)
If anyone wants to clarify this to me, thanks in advance.
produced by a collection of uniformly charged disks.
a+b) Given equations, sketch of problem
This is the equation in the handbook for a disk (but in the exercises the z becomes x, without loss of generality)
So by varying theta, he wants you to superpose the disks, to form a solid sphere. The disks are x- R* cos(theta) removed.
The Attempt at a Solution
[/B]
So he changes in the equation for the disk,the nominator z was the distance from the evaluation point to the center of the disk, this was z. This now becomes x-R*cos(theta). The denominator was the distance from the rim of the disk to the evaluation point, this was in the equation just the pythagoras rule, now it varies with theta because you have a superposition of different disks, so the pythagoras rule becomes the cosine rule. I kinda get these alterations.
What I don't get:
But I don't really get how he substitutes the surface charge density with this term with rho in? The term d(surface charge charge) = rho * R * sin (theta) * d(theta)
If anyone wants to clarify this to me, thanks in advance.
Last edited: