Electric field of a hollow cylinder

[Zack K]

Homework Statement

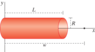
A thin-walled hollow circular glass tube, open at both ends, has a radius R and length L. The axis of the tube lies along the x axis, with the left end at the origin. The outer sides are rubbed with silk and acquire a net positive charge +Q distributed uniformly. Determine the electric field at a location on the x axis, a distance w from the origin. s

Relevant Equations

$E_{ring}=\frac{1}{4\pi\epsilon_0}\frac{Qz}{(R^2+z^2)^{3/2}}$

I uploaded a diagram of the problem.

I treated this as many thin rings and integrated it over the length. I placed my origin as in the same place as the uploaded picture.

Finding the electric field due to one small ring:

$\vec r =\langle w-x, 0, 0 \rangle$ where $x$ is the distance of the thin ring from the origin.
$|\vec r|= w-x$ $\therefore \hat r=1$

Now this is the spot where I'm sure I made a mistake. So using the equation of a thin ring, and representing that infinitesimally, we get:
$dE=\frac{1}{4\pi\epsilon_0}\frac{\Delta Q x}{(R^2+x^2)^{3/2}}$

$\Delta Q=Q\left(\frac{2\pi R\Delta x}{2\pi R L}\right)=Q\frac{\Delta x}{L}$

$dE=\frac{1}{4\pi\epsilon_0}\frac{(Q\frac{\Delta x }{L})x}{(R^2+x^2)^{3/2}}$

Integrating from $x=0$ to $x=L$:

$E=\frac{1}{4\pi\epsilon_0}\frac{Q}{L}\int_0^L \frac{x}{(R^2+x^2)^{3/2}}dx$

Solving that integral, we get:

$E=\frac{KQ}{2L}\left( -\frac{1}{\sqrt{R^2+L^2}}+\frac{1}{R} \right)$

This doesn't seem right at all, and I have no way of checking since my book doesn't have the answer for this. My classes are over and my professor is at some conference, and I can't use Gauss's Law to check my answer since the electric field at that point is pointing in different directions.

 

[SammyS]

I uploaded a diagram of the problem.

I treated this as many thin rings and integrated it over the length. I placed my origin as in the same place as the uploaded picture.

Finding the electric field due to one small ring:

$\vec r =\langle w-x, 0, 0 \rangle$ where $x$ is the distance of the thin ring from the origin.
$|\vec r|= w-x$ $\therefore \hat r=1$

Now this is the spot where I'm sure I made a mistake. So using the equation of a thin ring, and representing that infinitesimally, we get:
$dE=\frac{1}{4\pi\epsilon_0}\frac{\Delta Q x}{(R^2+x^2)^{3/2}}$

$\Delta Q=Q\left(\frac{2\pi R\Delta x}{2\pi R L}\right)=Q\frac{\Delta x}{L}$

$dE=\frac{1}{4\pi\epsilon_0}\frac{(Q\frac{\Delta x }{L})x}{(R^2+x^2)^{3/2}}$

Integrating from $x=0$ to $x=L$:

$E=\frac{1}{4\pi\epsilon_0}\frac{Q}{L}\int_0^L \frac{x}{(R^2+x^2)^{3/2}}dx$

Solving that integral, we get:

$E=\frac{KQ}{2L}\left( -\frac{1}{\sqrt{R^2+L^2}}+\frac{1}{R} \right)$

This doesn't seem right at all, and I have no way of checking since my book doesn't have the answer for this. My classes are over and my professor is at some conference, and I can't use Gauss's Law to check my answer since the electric field at that point is pointing in different directions.

Yes, It's not correct.

In the diagram you provided (see immediately below) it looks like $w$ may be the point of observation on the $x\text{-axis}$. That is to say, you intend to evaluate the electric field at $x=w\,.$

In that case your result should depend on $w$ .

In the Relevant equation you give,

$\displaystyle E_{ring}=\frac{1}{4\pi\epsilon_0}\frac{Qz}{(R^2+z^2)^{3/2}} \ ,$​

what do the variables represent? In particular, what does $z$ represent?

 

[Zack K]

In particular, what does zzz represen

My bad, $z$ represents an arbitrary location, $Q$ is the charge of the ring and $R$ is the radius of the ring.

In that case your result should depend on w

Yes that's what bothers me, my answer doesn't depend on a distance.

I think my mistake lies some where from the transition from
$E_{ring}=\frac{1}{4\pi\epsilon_0}\frac{Qz}{(R^2+z^2)^{3/2}}$ to $dE=\frac{1}{4\pi\epsilon_0}\frac{\Delta Q x}{(R^2+x^2)^{3/2}}$

Something that comes to mind, is that my distance vector is represented as $\vec r= \langle w-x, 0, 0 \rangle$, but in my transition from $E$ to $dE$ I stated above, I labelled the distance as simply $x$. Should it maybe be $w-x$ instead of just $x$?

 

[SammyS]

My bad, $z$ represents an arbitrary location, $Q$ is the charge of the ring and $R$ is the radius of the ring.Yes that's what bothers me, my answer doesn't depend on a distance.

I think my mistake lies some where from the transition from
$E_{ring}=\frac{1}{4\pi\epsilon_0}\frac{Qz}{(R^2+z^2)^{3/2}}$ to $dE=\frac{1}{4\pi\epsilon_0}\frac{\Delta Q x}{(R^2+x^2)^{3/2}}$

Something that comes to mind, is that my distance vector is represented as $\vec r= \langle w-x, 0, 0 \rangle$, but in my transition from $E$ to $dE$ I stated above, I labelled the distance as simply $x$. Should it maybe be $w-x$ instead of just $x$?

Yes, $z$ is something like that. Actually, $z$ is the distance from the point of observation to the plane containing the ring. That's the x-coordinate of your $\vec r$ vector. Right?

$x$ represents the location a slice of your cylinder (a ring) and $w$ is the location of the point of observation. (Both locations are on the x-axis.)

How far is each slice from the point of observation?

 

[Zack K]

How far is each slice from the point of observation?

Isn't it how I represented it? As $w-x$?

I'll try integrating this and see what I get.

 

[SammyS]

Isn't it how I represented it? As $w-x$?

I'll try integrating this and see what I get.

What $d$ ?

No. It's $(w-x)$, is it not?

 

[Zack K]

What $d$ ?

No. It's $(w-x)$, is it not?

Yes sorry I changed it, $d-w$ is from another problem stuck in my head.

So I carried out $E=\frac{1}{4\pi\epsilon_0}\frac{Q}{L}\int_0^L \frac{(w-x)}{(R^2+(w-x)^2)^{3/2}}dx$

Giving me: $E_x=\frac{1}{4\pi\epsilon_0}\frac{Q}{L}\left[\frac{1}{\sqrt{R^2+(w-L)^2}}-\frac{1}{\sqrt{R^2+w^2}}\right]$

Looks like it makes more sense, but doesn't look pretty. How exactly do I test to see if this makes sense? I can't think of any limit tests that will clarify if the result is valid.

 

[SammyS]

Yes sorry I changed it, $d-w$ is from another problem stuck in my head.

So I carried out $E=\frac{1}{4\pi\epsilon_0}\frac{Q}{L}\int_0^L \frac{(w-x)}{(R^2+(w-x)^2)^{3/2}}dx$

Giving me: $E_x=\frac{1}{4\pi\epsilon_0}\frac{Q}{L}\left[\frac{1}{\sqrt{R^2+(w-L)^2}}-\frac{1}{\sqrt{R^2+w^2}}\right]$

Looks like it makes more sense, but doesn't look pretty. How exactly do I test to see if this makes sense? I can't think of any limit tests that will clarify if the result is valid.

That looks good.

Let $R \to 0$ .