Electric field of a positive plate

[doggydan42]

1. Homework Statement
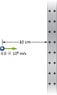
There is a large positively charged plate whose charge density is $\sigma = 2.0 × 10^{-5}\frac{C}{m^2}$. What is the electric field at a point P, that is not enclosed between the plates.

2. Homework Equations
For an infinite sheet:
$$\vec E = \frac{\sigma}{2\varepsilon_0}\hat r$$

3. The Attempt at a Solution
I thought to find the field of the plate by adding, but that would be the field between two infinite planes, one with negative charge and one with a positive charge. Would that still form the electric field of a positively charged plate? So,
$$\vec E = \frac{\sigma}{\varepsilon_0}\hat r$$

Thank you in advance.

 

[TSny]

Hello. Can you clarify the problem statement? The first sentence seems to imply that there is only one plate. The second sentence implies more than one plate.

 

[doggydan42]

There is one plate. The plate has three dimensions, while the sheet only has two. So there is a thickness to the plate that the sheet does not have.

 

[doggydan42]

Hello. Can you clarify the problem statement? The first sentence seems to imply that there is only one plate. The second sentence implies more than one plate.

The plate has a thickness, so it is in three dimensions. The sheet is only two dimensional, so it would be a plane in a 3D space.

 

[TSny]

There is one plate. The plate has three dimensions, while the sheet only has two. So there is a thickness to the plate that the sheet does not have.

So you have a single plate that has some thickness to it? What does it mean when the problem statement says that point P is not between the plates?

 

[doggydan42]

Well I did not state the full problem, but if it helps here's an image. Part of the problem was finding the electric field to find the force, and once I find that I know how to continue. So the proton is not between the two sheets which form the plates.

 

[TSny]

OK, that helps. Point P is not between the faces of the plate. In the problem statement, you say that $\sigma$ is the charge density of the plate. Does that mean that each face of the plate has the surface charge $\sigma$?

I think it would be helpful to state the relevant part of the problem word for word.
See the paragraph for item 3 here: https://www.physicsforums.com/threads/guidelines-for-students-and-helpers.686781/

 

[doggydan42]

The whole problem is:
From a distance of 10 cm, a proton is projected with a speed of v = 4.0 × 106 m/s directly at a large, positively charged plate whose charge density is $\sigma = 2.0 × 10^{−5}C/m^22$. (See below.) (a) Does the proton reach the plate? (b) If not, how far from the plate does it turn around?

So from my understanding, $\sigma$ would be the surface charge of each plate.

 

[TSny]

Thank you. You have the right idea that you sum the contributions from each surface (sheet of charge). Your expression for E in the "attempt at a solution" is correct, although I'm not sure what the unit vector $\hat r$ denotes?

 

[doggydan42]

$\hat r$ would be the direction of the field.

Thank you.

 

[TSny]

$\hat r$ would be the direction of the field.

And what direction would that be?

 

[doggydan42]

In this case it would be in the $-\hat i$ direction acting on the proton.

 

[TSny]

In this case it would be in the $-\hat i$ direction acting on the proton.

OK. Good. I think you have it.