SUMMARY
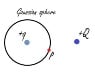
This discussion clarifies the application of Gauss' Law in determining the electric field at a point P due to an enclosed charge +q and an external charge +Q. It establishes that while Gauss' Law can calculate the electric field due to the enclosed charge, it does not account for the influence of external charges on the net electric field at point P. The key takeaway is that the electric field at point P is derived from the superposition of the fields from both charges, but only the enclosed charge contributes to the net flux through the Gaussian surface, as the flux due to external charges is zero.
PREREQUISITES
- Understanding of Gauss' Law and its mathematical formulation:
∫ \vec{E} \cdot d\vec{A} = \frac{q}{\epsilon_{0}}
- Knowledge of electric field concepts and vector addition
- Familiarity with the principle of superposition in electrostatics
- Basic understanding of electric flux and its implications in electromagnetism
NEXT STEPS
- Study the implications of Gauss' Law in different symmetrical charge distributions
- Learn about electric field calculations using the superposition principle in complex charge systems
- Explore the concept of electric flux in greater detail, including its applications in various geometries
- Investigate the relationship between electric field lines and charge distributions in electrostatics
USEFUL FOR
This discussion is beneficial for physics students, educators, and anyone interested in deepening their understanding of electrostatics, particularly in applying Gauss' Law to analyze electric fields in the presence of multiple charges.