tyreal
- 3
- 0
Homework Statement
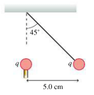
A 0.020g plastic bead hangs from a lightweight thread. Another bead is fixed in position beneath the point where the thread is tied. If both beads have charge q, the moveable bead swings out to the position shown (attachment). What is q?
Homework Equations
F=[K(q1)(q2)]/r^2
w=mg
The Attempt at a Solution
I am new to physics forums so please excuse my equations formatting! I know this is a force balancing problem. I think that tension force of string equals weight force of bead. There is a repulsive electrical force between the two beads, which I think equals the tension/gravitational force that is holding the bead in place.
T=mg=0.000196N
My question is, should I set this equal to the expression of [K(q1)(q2)]/r^2 and solve for q? I know that is the last step since I am trying to find q. BUT, my professor said we had to use sin45 or cos45 in some way so as to separate the x and y components of the force. I don't see where to incorporate that. I am missing some sort of middle step here, any input would be appreciated!