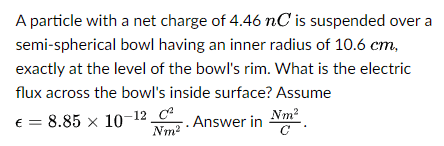Homework Help Overview
The discussion revolves around calculating the electric flux through a semi-spherical bowl from a charged particle, incorporating aspects of calculus and Gauss's Law. Participants are exploring the implications of the problem's setup, including the position of the charged particle and the surface area of the bowl.
Discussion Character
- Exploratory, Assumption checking, Conceptual clarification
Approaches and Questions Raised
- Participants discuss the symmetry of the problem and the equations relevant to electric flux. There are inquiries about the surface area of the hemisphere and the implications of the dielectric constant of the bowl material. Some participants express uncertainty about using Gauss's Law and how to account for the hemisphere in calculations.
Discussion Status
The discussion is active, with participants providing guidance on relevant equations and questioning the clarity of the problem statement. There are multiple interpretations being explored regarding the dielectric properties and the application of Gauss's Law, with no explicit consensus reached yet.
Contextual Notes
Participants note the lack of specification regarding the dielectric constant of the bowl material, which raises questions about its impact on the electric field and the calculations involved. There is also mention of the need to consider the hemisphere's surface area in relation to the full sphere.