Electric Flux through a sphere from a point charge

[deedsy]

Homework Statement

I need to create an equation that can tell me the electric flux through the surface of a sphere (centered at the origin) due to a point charge placed at various locations in/around the sphere. For example, find the electric flux through the sphere (of radius = 1) with a point charge placed at (1,0.5,0) --> these are (x',y',z') aka the location of the point charge.

* I realize this can be easily solved using Gauss Law, but I cannot use that and need to rigorously prove the solutions with a double integral (see below)

Homework Equations

*see below

The Attempt at a Solution

The strategy I'll be using for this problem will be to calculate \oint \vec{E}\cdot d\vec{A} over the surface of the sphere. So for the sphere, d\vec{A} = r^2 sin(\theta) d\theta d\phi.

Also, in spherical coordinates, the potential is (with x',y',z' the location of the point charge relative to the origin (the center of the sphere)): V(r,\theta,\phi) = \frac{q}{4 \pi ε_0} \frac{1}{\sqrt{(r sin(\theta)cos(\phi) - x')^2 + (r sin(\theta)sin(\phi) - y')^2 + (r cos(\theta) - z')^2}}

We also know that: E(r,\theta,\phi) = -\nabla V(r,\theta,\phi)

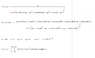
So, as you can see in my attached image (from Mathcad - i wrote (x',y',z') as (xp,yp,zp)) the integral that I believe should give me what I want is:
E = \int_0^{2\pi} \int_0^\pi -\nabla_r V(r,\theta,\phi) r^2 sin(\theta) d\theta d\phi
where I have assumed that E_r is the only component of the flux I should be concerned with (perhaps this is my error??)

Now I should be able to change my (x',y',z') (xp,yp,zp in Mathcad) values for the location of the point charge, and my integral should give me the correct electric flux through the sphere due to it. For example, with a sphere radius = 1, and point charge located at (x',y',z')=(0.3,0,0) I should get simply E = \frac{q}{ε_0}. With (x',y',z')=(2,0,0), I should get E = 0. For (x',y',z')=(1,0,0) - the point charge right on the surface of the sphere, I should get E = \frac{q}{2 ε_0}.

Unfortunately, I've waited for Mathcad to evaluate this integral for 15 minutes, and it's still working on it, so I don't think it's correct. Did I set this problem up correctly??

 

[Greg Bernhardt]

Thanks for the post! Sorry you aren't generating responses at the moment. Do you have any further information, come to any new conclusions or is it possible to reword the post?

 

[deedsy]

Thanks for the post! Sorry you aren't generating responses at the moment. Do you have any further information, come to any new conclusions or is it possible to reword the post?

Hey, thanks for the concern, but I actually figured this one out. It was more a problem with Mathcad than my method. The method I posted above was the right way to go about the problem